AHC036参加記

2024/09/02

RECRUIT 日本橋ハーフマラソン 2024夏（AtCoder Heuristic Contest 036）（以下AHC036）の参加記です。普段はAtCoderを使っていないのですが、長期コンがあればいつか参加したいと思っていました。

とはいえAHC036の存在に気付いたのが当日だったので、事前に参加登録がいるのかよく分からず焦ったり、ルールに「制限時間以内に1問でも多く解いた人が優勝です。正答数が同じ場合は早く解いた人の方が上の順位になります。」と書いてあるのを読んでスコアコンじゃないのか心配になったり、てんやわんやな参加となりました。

AHCに参加するのは初めてですが、以前長期コンを求めて過去問を漁っていた時にAHC033をupsolveしたので何となくのイメージは持っています（当時のバーチャル参加記はこちら）。乱択くらいしかスコアコンに使えそうなテクニックを持っていませんが、持ち前の明るさでカバーしていこうと思います。

なおこの参加記は、最初からコンテスト中のデバッグと考察に使用する目的で書いているため情報の取捨選択が少なくかなり重めです。

問題文

問題文そのものはこちらからご確認いただけます。

大雑把に言うと、$600$頂点高々$1800$辺の平面グラフである連結無向グラフ$G$があって、指定された頂点の列に沿って$G$上でスタンプラリーを行うというものです。ただし頂点にはON/OFFの状態があり、OFFの頂点には移動できず、所定の操作で頂点のON/OFFを切り替えて移動します。この問題で要求されていることは、スタンプラリーを最後まで終えた時点でのON/OFFの切り替え操作の回数の最小化です。ただし移動とON/OFF切り替え操作の合計回数は$10^5$回以下に抑える必要があります。

各頂点のON/OFFの管理には数列$B$が使われ、頂点がONである必要十分条件はその頂点番号が$B$の成分に現れることです。最初は$B$の各成分が$-1$であり、つまり全ての頂点がOFFの状態です。

ON/OFFの切り替え操作には長さだけ指定された数列$A$が使われます。$A$の成分は自分で好きに決めてよく、全ての操作より前に固定します。ON/OFFの切り替え操作は、同じ長さになるように$A$と$B$の連続部分列を好きに選んで後者を前者で置き換えるというものです。

それでは挑戦してみましょう。

$1$日目（8/23金）

この日ははちじさん主催のyukicoder contest 441でした。yukicoderメインで活動しているのでyukicoder優先で、この日はAHC036の参加登録だけは済ませ、yukicoderコンテスト前に軽く問題文を読むだけにしておきました。

なおyukicoderの結果は（A,Bはtesterで）C,Dの2完でした。3完を目指していましたが、眠すぎて何度か眠気覚ましに時間を割いたのですがラスト１時間は目が霞んでしまいEはまともに問題文が読めませんでした。

$2$日目（8/24土）

前日に解けなかったE問題を解説読みACして、AHC036に挑戦です。最初は自明な点を取る（得点を稼ぐための行動は何もしないが少なくとも正解ではある）提出をしてそこを起点にしていくつもりでしたが、何だか自明な点を取るのがそんなに簡単ではなさそうです。

となると自明な点を取るコードを書くのも何だか利点が少なさそうなので、ある程度は点数を考えたコードを書いていこうと思います。

なお来週は忙しいので、土日の間になるべく提出を頑張りたいところ。ACまで辿り着きたいなあ。

$1$回目の提出

とりあえずの方針は

まず何かしらの点数取ることを目標にしつつ、実装難度が変わらなそうな改良点があれば最初からそれを採用する。
ついでに「これは手抜きだなあ」と思うところにコメントをつけておき、後で改良する際の参考にする。
そこからコメントを参考にして徐々に点数を伸ばす。
コメントが完全になくなったら、改めて本格的に考察をする。

という感じでいこうと思います。

1に関して裏を返せば、実装難度が変わりそうな手抜きがあれば遠慮なく手抜いていこうという寸法です。具体的には

$A$は（スタンプラリーの成功可能性を担保するために）$(0,\ldots,599)$を先頭に入れて残りは乱択にでもしておく。
ON/OFF切り替え操作では連続部分列の長さを$1$に固定し、$B$の連続部分列は先頭から取ることに固定する。
$2$スタンプ間の経路探索では、道中のON/OFF操作の切り替えを無視して始端側のスタンプ到達時点でのON/OFFの状態のみを利用してOFFの辺を通る回数が最小となる経路を01BFSで計算。

の$3$つを試みました。これでもまだまだ実装が重いですけど、何とか実装が終わりました。

実行時間の使いどころが難しいですが、ひとまず「$A$の末尾$L_A- N$項を決めるごとにON/OFF切り替え操作の合計回数を計測する」という処理のループにしてみました。

ただしコードテストで出力を作成し、ビジュアライザに与えてみるとバグがいっぱいあったのでまだまで提出できません。

たくさんのバグを取ったのですが、どうにも詰まってしまいました。何故かスタンプラリーを終えてくれません。何故？

色々考えた結果、コードテストでは出力が途中で打ち切られるのではないかという結論に至り、自環境でファイルを書き出すことにしました。すると余計な文字列がいっぱい書き込まれていきます。自環境ではデバッグ用に大量の出力をするように設定していたので、そこを直さなきゃいけない。何だかとても面倒くさくなってきました。ビジュアライザに渡すの、出力じゃなくて提出コードにしてくれるサービス募集中です。

それでも何とか頑張って、ようやくビジュアライザ上で最後まで走ってくれる出力が作れました！（ビジュアライザの画像は後述の理由で省略します）

というわけでいざ初提出！

以下、マクロだらけで役に立たないと思いますがC++のソースコードの定義本体部分です。

実際の提出ページはこちらです。

IN VO Solve()
{
  CEXPR( int , bound_N , 600 );
  CEXPR( int , bound_T , 600 );
  CEXPR( int , bound_LB , 24 );
  CIN_ASSERT( N , bound_N , bound_N );
  CIN_ASSERT( M , N - 1 , 3 * ( N - 2 ) );
  CIN_ASSERT( T , bound_T , bound_T );
  CIN_ASSERT( LA , N , 2 * N );
  CIN_ASSERT( LB , 4 , bound_LB );
  vector<vector<int>> e( N );
  REPEAT( M ){
    CIN( int , u , v );
    e[u].push_back( v );
    e[v].push_back( u );
  }
  CIN_A( int , 1 , T , target );

  vector<int> hind;
  auto edge = [&]( const int& u ){
    vector<T2<int>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] > 0 ? 0 : 1 } );
    }
    return answer;
  };
  Graph graph{ N , edge };
  ZeroOneBreadthFirstSearch bfs{ graph , -1 };

  // O(N+M)
  auto Path = [&]( const int& t ){
    // O(M)
    // (!)現時点での信号の状況しか考慮せずに最短径路探索
    while( bfs.Next() != target[t+1] ){}
    vector<int> path{ target[t+1] };
    // O(N)
    while( true ){
      auto& u = bfs.prev( path.back() );
      if( u == target[t] ){
	break;
      }
      path.push_back( u );
    }
    return path;
  };

  // O(N)
  vector<int> A( LA );
  vector<vector<int>> A_inv( N );
  vector<int> B{};
  FOR( i , 0 , N ){
    A_inv[A[i] = i].push_back( i );
  }
  auto InitialiseArray = [&](){
    FOR( i , 0 , N ){
      A_inv[i].resize( 1 );
    }
    FOR( i , N , LA ){
      A_inv[A[i]].push_back( i );
    }
    B = vector<int>( LB , -1 );
    hind = vector<int>( N );
  };

  auto SetOperation = [&]( const int& v , int& count , vector<vector<int>>& query ){
    count++;
    // (!)A_inv[v]の末尾に固定
    auto itr = --A_inv[v].end();
    int j , L;
    if( B[0] == -1 ){
      j = 0;
      L = LB;
      if( v + L > LA ){
	itr = A_inv[LA-L].begin();
      } else {
	while( *itr + L > LA ){
	  --itr;
	}
      }
    } else {
      // (!)Bの先頭に固定
      j = 0;
      // (!)長さ1固定
      L = 1;
    }
    query.push_back( { L , *itr , j } );
    FOR( l , 0 , L ){
      if( B[j+l] != -1 ){
	hind[B[j+l]]--;
      }
      hind[B[j+l] = A[*itr+l]]++;
    }
  };

  // O(T(N+M))
  auto SimulateTavel = [&](){
    int count = 0;
    vector<vector<int>> query{};
    // O(N)
    InitialiseArray();
    // O(T(N+M))
    FOR( t , 0 , T ){
      // O(N)
      bfs.Initialise( target[t] );
      // O(N)
      auto path = Path( t );
      while( !path.empty() ){
	// (!)次の頂点しか考慮せずに信号操作
	int v = path.back(); path.pop_back();
	if( hind[v] == 0 ){
	  SetOperation( v , count , query );
	}
	query.push_back( { v } );
      }
    }
    return pair<int,vector<vector<int>>>{ count , move( query ) };
  };
  
  START_WATCH;
  int repetition = 0;
  vector<int> A_opt( LA - N );
  int count_min = 1e9;
  vector<vector<int>> query_opt{};
  while( CHECK_WATCH( 3000 ) ){
    // O(N)
    unordered_set<int> A_memory{};
    FOR( i , N , LA ){
      int temp;
      // (!)Aが適当
      while( A_memory.count( temp = GetRand( 0 , N - 1 ) ) == 1 ){}
      A_memory.insert( A[i] = temp );
    }
    // O(T(N+M)), T(N+M) <= 1440000
    auto [count,query] = SimulateTavel();
    repetition++;
    if( count_min > count ){
      FOR( i , N , LA ){
	A_opt[i-N] = A[i];
      }
      count_min = count;
      query_opt = move( query );
      COUT( "#trial" , repetition , ":" , count );
    }
  }
  COUT( "#trial count:" , repetition );
  FOR( i , N , LA ){
    A[i] = A_opt[i-N];
  }
  COUT( A );
  RUN( query_opt , q ){
    COUT( q.size() == 1 ? 'm' : 's' , q );
  }
}

結果はAC×45、TLE×5です。TLが$3000$[ms]でループ処理を$2900$[ms]で打ち切っているのですが、実行時間は$3310$[ms]でした。何で？

$2$回目の提出

仕方ないので、ループ処理を$2400$[ms]に縮めることにしました。なお一番最初のON/OFF切り替えだけは連続部分列の長さを$4$にしていたのですが、$A$の末尾$4$項次第でバグることに気付いたのでそこも修正。（このバグは配列外参照なので未定義動作ですが、TLEの原因ではないだろうと期待します）

再提出は$30$[m]空けないといけないので、解消可能な手抜きを解消していきます。

まずは、ON/OFF切替時の連続部分列の長さを$1$固定にしていたのをやめることにしました。

$2$スタンプ間の経路は第$1$提出と同様に始端側のスタンプ到達時点でのON/OFFの状態のみを利用して01BFSで計算し、その経路を進むと決めた上で道中ではON/OFF切替時の連続部分列を貪欲に（経路中に通る頂点をなるべくONにするように）決めることにします。

ただし連続部分列は相変わらず$B$の先頭から取ることにしました。手抜きです。

それでもビジュアライザによると若干スコアは良くなったようです。貪欲に選んでもほぼ毎回連続部分列の長さが$1$になるようですが、$1$回だけ長さ$4$で更新していました。

さて、実装が遅いのでこの更新だけでもう提出可能な時間です。

結果はAC×48、TLE×2です。ループ処理を$2400$[ms]で打ち切っているのに、実行時間は$3225$[ms]でした。何で？

$3$回目の提出

これあれかな、もしかして$1$回のループが$800$[ms]くらいかかってるケースが混ざってる？　ビジュアライザのサンプルでは$43$回もループできているのでそんなことないと思うのですが。一応ループの時間も計測して、それに合わせて打ち切る時間を変えてみましょうか。$2000$から平均ループ時間を引いたくらいで。

変更点は

  while( CHECK_WATCH( 2500 ) ){

を

  double curr = CURRENT_TIME;
  while( CHECK_WATCH( 2000 - ( repetition > 0 ? int( ( curr - CURRENT_TIME ) / repetition ) : 0 ) ) ){

にするだけの簡単なお仕事。

……ですが結果はAC×49、TLE×1です。実行時間は$3170$[ms]でした。何で？

$4$回目の提出

完全に手詰まりなので、強い競技プログラマーだったらどう助言してくれるかを思い浮かべます。

イマジナリーShirotsumeさん「これはループ継続か否かを決める計時より後に時間が掛かりすぎてますね。大会ならジャッジ呼ばれるレベルの遅延です」

……それだ！　出力回数は$\Theta(TN)$で、最悪ケースは線形グラフの両端を行き来するパターン。定数倍は$6$倍かかるし、これそこそこ重い！　何で気が付かなかったんだろう。

というわけで、打ち切る時間に出力回数も込めることにしました。

  double curr = CURRENT_TIME;
  while( CHECK_WATCH( 2000 - ( repetition > 0 ? int( ( curr - CURRENT_TIME ) / repetition ) : 0 ) ) ){

を

  double curr = CURRENT_TIME;
  while( CHECK_WATCH( 2000 - int( query_opt.size() ) / 4000 - ( repetition > 0 ? int( ( curr - CURRENT_TIME ) / repetition ) : 0 ) ) ){

に変更するだけで提出です。

……結果はAC×47、TLE×3です。実行時間は$3274$[ms]で悪化しました。何で？

あれ？　でも順位表見ると何か得点が入ってる扱いになってる。「自分の得点状況」ページでは$0$点なのに。どういうことなの……？

ルールを読み返してみたら、TLEしてもそのケースを除いた得点が得られるらしい。じゃあ何で「自分の得点状況」ページでは$0$点の表示なんだろう。

とりあえず現時点で$6,776,220,315$点で230/432位らしい。AC取れてない人もいっぱいいるわけですね。周りは色とりどりですが、お隣さんも黒色でした。親近感が湧きますね。

$5$回目の提出

何はともあれACを取ることを目標に、十分余裕を持って$1000$[ms]で打ち切ってしまうことにしました。

  double curr = CURRENT_TIME;
  while( CHECK_WATCH( 2000 - int( query_opt.size() ) / 4000 - ( repetition > 0 ? int( ( curr - CURRENT_TIME ) / repetition ) : 0 ) ) ){

を

  while( CHECK_WATCH( 1100 ) ){

に変更です。

ここでようやくAC！　長かった・・。実行時間は$2926$[ms]、本当にギリギリです。現時点で$7,056,328,946$点、224/496位です。周りには黒色もちらほら。

$6$回目の提出

ここからは

実行時間が想定外な理由を特定する。
どこをループさせるかをガラッと変えることで実行時間が想定外だった理由を考えずに済むようにする。

の$2$通りの方向性があります。魅力的なのは後者ですが、その前にループ回数を$1$回だけにしてみて実行時間がどう変化するかを確認してみようと思います。もしループ回数$1$回にしても実行時間があまり減らないならば、他の箇所をループさせるとTLEするリスクが高いですからね。

あと01BFSで辺に持たせる重みは$0,1$値でもbool値でも良いですが、bool値の方がメモリが小さいのでbool値に変更します

というわけで

    vector<T2<int>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] > 0 ? 0 : 1 } );
    }
  /* 省略 */
  while( CHECK_WATCH( 1100 ) ){

を

    vector<pair<int,bool>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] > 0 } );
    }
  /* 省略 */
  // while( CHECK_WATCH( 1100 ) ){
  while( repetition == 0 ){

に変えてみます。結果はAC×33、WA×17で実行時間$2938$[ms]です。WAは恐らくループが$1$回になったためON/OFF切り替え回数が大きくなり、移動回数との合計が上限の$10^5$回を超えてしまったのでしょう。注目すべきは実行時間で、ループが$1$回でも全然変わっていません。つまり、打ち切る時間を縮めるとか関係なかったわけですね。$1$回目のループ開始の計時時点では時間が十分余っているのでループが始まるわけですが、計時より後の$1$回目のループ本体がそもそも重かった、と。

あれ？　そういえばさっき何てセリフを思い浮かべましたっけ？

あー！　計時より後に時間が掛かってるって……出力じゃなくて、$1$回目のループ本体の話だった！

そこで気付いたのが、$A$の乱択部分のひどさ。

    FOR( i , N , LA ){
      int temp;
      // (!)Aの末尾が適当
      while( A_memory.count( temp = GetRand( 0 , N - 1 ) ) == 1 ){}
      A_memory.insert( A[i] = temp );
    }

よく見たら$A$の末尾に重複が出ないように乱択する処理がめちゃくちゃひどく、$O(N)$を書いていたつもりが「ランダムに選び、既に選ばれていたら繰り返す」という平均$O(N^2)$の絶望的な挙動になってる！　これはなるほど、ループさせれば運悪くめちゃくちゃ時間を食ってしまうパターンに陥りそうです。テストケース作るときでさえやらないようなミスをやってしまいました。

    FOR( i , N , LA ){
      // (!)Aの末尾が適当
      A[i] = GetRand( 0 , N - 1 );
    }

これで高速になるはずです。WAは出るかもしれませんがとりあえず投げてみます。

結果はAC×31、WA×19で、実行時間$52$[ms]！　光明が開けました。

$7$回目の提出

さて、これまでは$A$の先頭$N$項を$(0,\ldots,N-1)$固定にして、残りを乱択にしていました。そして「$A$の末尾$L_A- N$項を決めるごとにON/OFF切り替えの回数を計算」をループさせていました。しかしどうもあまりループの寄与が大きくない。ループなしだとWAになってしまうので寄与がないわけではないですが、ビジュアルエでディタのサンプルを見る限り何十回かループさせても回数の更新は数回しか起こらなさそう。

というわけで今度は、$A$の先頭$N$個の決め方も変えていこうと思います。具体的には、グラフ$G$上で近い頂点の番号同士が$A$の中でも近くなるように取りたいです。

親切にも今回は$G$が平面グラフなので、射影によって近さを保つ（遠さは保たない）番号付け直しが可能です。「射影方向を乱択し、それによる番号付けで$A$の先頭$N$項を決め、残りを乱択する」という方法で$A$を決めることにして、「$A$を決めるごとにON/OFF切り替えの回数を計算」をループしてみようと思います。

実装はできたのですが、ビジュアライザが何故か動きません（「ページは応答していません」の警告が出てフリーズする）。仕方ないのでビジュアライザを使わず提出してみることに。

以下、C++のソースコードの定義本体部分です。

実際の提出ページはこちらです。

  START_WATCH;
  CEXPR( int , bound_N , 600 );
  CEXPR( int , bound_T , 600 );
  CEXPR( int , bound_LB , 24 );
  CIN_ASSERT( N , bound_N , bound_N );
  CIN_ASSERT( M , N - 1 , 3 * ( N - 2 ) );
  CIN_ASSERT( T , bound_T , bound_T );
  CIN_ASSERT( LA , N , 2 * N );
  CIN_ASSERT( LB , 4 , bound_LB );
  vector<vector<int>> e( N );
  REPEAT( M ){
    CIN( int , u , v );
    e[u].push_back( v );
    e[v].push_back( u );
  }
  CIN_A( int , 1 , T , target );
  CIN_A( T2<int> , 0 , N , xy );

  vector<int> hind;
  auto edge = [&]( const int& u ){
    vector<pair<int,bool>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] > 0 } );
    }
    return answer;
  };
  Graph graph{ N , edge };
  ZeroOneBreadthFirstSearch bfs{ graph , -1 };

  // O(N+M)
  auto Path = [&]( const int& t ){
    // O(N)
    bfs.Initialise( target[t] );
    // O(M)
    // (!)現時点での信号の状況しか考慮せずに最短径路探索
    while( bfs.Next() != target[t+1] ){}
    vector<int> path{ target[t+1] };
    // O(N)
    while( true ){
      auto& u = bfs.prev( path.back() );
      if( u == target[t] ){
	break;
      }
      path.push_back( u );
    }
    return path;
  };

  // O(N)
  vector<int> A{};
  vector<vector<int>> A_inv( N );
  vector<int> B{};
  vector<T2<int>> line( N );
  auto InitialiseArray = [&](){
    if( A.size() == 0 ){
      A.resize( LA );
    }
    int c_x = GetRand( -10 , 10 );
    int c_y = GetRand( -10 , 10 );
    FOR( i , 0 , N ){
      auto& [x,y] = xy[i];
      line[i] = { c_x * x + c_y * y , i };
    }
    Sort( line );
    FOR( i , 0 , N ){
      A_inv[A[i] = line[i].second] = { i };
    }
    FOR( i , N , LA ){
      A_inv[A[i] = GetRand( 0 , N - 1 )].push_back( i );
    }
    B = vector<int>( LB , -1 );
    hind = vector<int>( N );
  };

  auto UpdateB = [&]( const int& L , const int& i , const int& j , vector<vector<int>>& query ){
    query.push_back( { L , i , j } );
    FOR( l , 0 , L ){
      if( B[j+l] != -1 ){
	hind[B[j+l]]--;
      }
      hind[B[j+l] = A[i+l]]++;
    }
  };

  auto FillB = [&]( const int& v , vector<vector<int>>& query ){
    auto begin = A_inv[v].begin() , itr = --A_inv[v].end();
    int i = *itr , j = 0 , L = LB;
    while( i + L > LA ){
      if( itr != begin ){
	i = *--itr;
      } else {
	i = LA - L;
      }
    }
    UpdateB( L , i , j , query );
  };

  auto OptimiseB = [&]( const int& v , const int& path_size , const vector<int>& path , vector<vector<int>>& query , Set<int>& vertex ){
    int i_opt = -1 , j = 0 , L_opt = 1 , hit_opt = -1;
    RUN( A_inv[v] , i ){
      int L_max = min( 4 , LA - i ) , hit = 0;
      FOREQ( L , 1 , L_max ){
	hit += ( L == 1 || path[path_size - ( L - 1 )] == A[i] ? 1 : 0 ) - vertex.count( B[L-1] );
	if( hit_opt < hit ){
	  i_opt = i;
	  L_opt = L;
	  hit_opt = hit;
	}
      }
    }
    UpdateB( L_opt , i_opt , j , query );
  };
  
  auto SetOperation = [&]( int& path_size , vector<int>& path , int& count , vector<vector<int>>& query , Set<int>& vertex ){
    // (!)次の頂点しか考慮せずに信号操作
    int v = path.back(); path.pop_back(); path_size--;
    if( hind[v] == 0 ){
      count++;
      // (!)A_inv[v]の末尾に固定
      if( B[0] == -1 ){
	FillB( v , query );
      } else {
	OptimiseB( v , path_size , path , query , vertex );
      }
    }
    query.push_back( { v } );
  };

  // O(T(N+M))
  auto SimulateTavel = [&](){
    int count = 0;
    vector<vector<int>> query{};
    // O(T(N+M))
    FOR( t , 0 , T ){
      // O(N)
      auto path = Path( t );
      Set<int> vertex{};
      RUN( path , v ){
	vertex.insert( v );
      }
      int path_size = path.size();
      while( path_size > 0 ){
	SetOperation( path_size , path , count , query , vertex );
      }
    }
    return pair<int,vector<vector<int>>>{ count , move( query ) };
  };
  
  int repetition = 0;
  vector<int> A_opt{};
  int count_min = 1e5;
  vector<vector<int>> query_opt{};
  while( CHECK_WATCH( 3000 ) ){
    // O(N)
    InitialiseArray();
    // O(T(N+M)), T(N+M) <= 1440000
    auto [count,query] = SimulateTavel();
    repetition++;
    if( count_min > count ){
      A_opt = move( A ); A.clear();
      count_min = count;
      query_opt = move( query );
      COUT( "#trial" , repetition , ":" , count );
    }
  }
  COUT( "#trial count:" , repetition );
  // O(N)
  COUT( A_opt );
  // O(TN), TN <= 360000
  RUN( query_opt , q ){
    COUT( q.size() == 1 ? 'm' : 's' , q );
  }
}

提出結果はAC×45、WA×5で実行時間は$2943$[ms]でした。うーん、もしかして移動回数とON/OFF切り替え回数の合計の上限$10^5$とは別の理由でWAになっているのかも？　こういう時にビジュアライザが回せないの厳しいですね……。ジャッジを書くべき？

ひとまずビジュアライザのWindows用のコンパイル済バイナリというものをダウンロードしてみました。vis.htmlというものに出力のビジュアライズ結果が書き出されるとあるのですが、vis.htmlを開いても白紙。何で？

$8$回目の提出

とりあえずWAが回数上限によるものと信じて考察。射影は平面上で近い頂点を近くに写しますが、辺で結ばれている$2$頂点が隣接してくれるとは限りません。とはいえ$(0,\ldots,N-1)$よりはましなはず？

よく分からないので、今度は辺で結ばれている$2$頂点が隣接する頻度が高くなるようにDFSで番号付けてみました。ビジュアライザが応答しなくても何分か待てばフリーズが解消されることに気付いたので試すと、むしろ悪化してそうです。

どうも眺めてみたところ、ON/OFF切替時に貪欲に取り替えると$B$の成分の後ろ$3$つが同じような位置に固まってしまい、その後なかなか活躍できないという状況に陥っている感じがします。貪欲に取り替えずに長さが$1$固定だった方がまだ役に立ってたのかも。

というわけで一旦長さ$1$に戻して考察し直そうかと思います。代わりに、$B$の初期値をなるべく強くするように、最初にBFSで各2スタンプ間の最短経路を調べておいて最短経路で最も通過される点を$B$に加えるようにしてみます。

結果はAC×32、WA×18で実行時間$2947$ms。だいぶ悪化しました。

本日（というか途中で寝落ちしたので既に翌日ですが）はここでお休みです。

$3$日目（8/25日）

明日からあまり時間が取れなくなるので、今日が頑張りどころです。

今日はyukicoderでイレギュラーな日程のコンテスト（普段は金曜ですが今日はオンサイトコンテストのミラーのようです）がありますが、金曜以外はまとまった時間を確保できないのでお休みします。

細かい時間なら確保できるので、そこをAHC036の考察と実装に当てていきます。

まずは昨日唯一のACだった$5$回目の提出（$A$の先頭が$(0,\ldots,N-1)$固定で残りを重複なく乱択、ON/OFF切り替え操作で選ぶ連続部分列は$B$の左端から貪欲に、ループ打ち切り$1000$[ms]）を観察してみます。

ここまでビジュアライザの出力結果を保存していなかったので出力し直しです。ところがビジュアライザの出力結果を保存する機能、めちゃくちゃ遅いですね……。50% finishedまではすぐいくのですが、そこからずっと止まってしまいます。$9$時間経っても変化がないようです。これが不具合なのか自環境の問題なのか分からず、かといって人に聞くのも不正になりそうなので駄目元でclarを投げてみました。

保存は一旦諦めて続けます。まず$5$回目の提出のビジュアライザのサンプルではON/OFF切り替え回数が$6026$回でした。ループ打ち切りが長くてTLEした$4$回目までの提出はもちろんもっと回数が少ないです。

一方で$6$回目以降の提出は$40000$回超えです。めちゃくちゃ差がありますね。もしかして最短経路を何故か計算できていない？　$5$回目と$6$回目の違いは

    vector<T2<int>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] > 0 ? 0 : 1 } );
    }
  /* 省略 */
  while( CHECK_WATCH( 1100 ) ){

を

    vector<pair<int,bool>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] > 0 } );
    }
  /* 省略 */
  // while( CHECK_WATCH( 1100 ) ){
  while( repetition == 0 ){

変えただけだから……あ！　辺の重みのbool値が逆！　先日の最後（$8$回目）の提出（DFS順に頂点を$A$に格納、DFS開始点を乱択して$2900$[ms]打ち切りループ、連続部分列は$B$の先頭から長さ$1$固定）からここを修正してみたら、ビジュアライザのサンプルのON/OFF切り替え回数が$6079$回に減りました。

$1$回目の提出

というわけで実行時間が遅かった原因はON/OFF切替時の連続部分列を貪欲に選んでいたせいではなかったので、改めて昨日の$7$回目の提出（射影順に頂点を$A$の先頭$N$項に格納して残りは乱択、射影の向き乱択して$2900$[ms]打ち切りループ、連続部分列は貪欲に選択）に戻してみます。ビジュアライザのサンプルのON/OFF切り替え回数が$5929$回に減りました。試しに提出してみましょう。

以下、C++のソースコードの定義本体部分です。

実際の提出ページはこちらです。

IN VO Solve()
{
  START_WATCH;
  CEXPR( int , bound_N , 600 );
  CEXPR( int , bound_T , 600 );
  CEXPR( int , bound_LB , 24 );
  CIN_ASSERT( N , bound_N , bound_N );
  CIN_ASSERT( M , N - 1 , 3 * ( N - 2 ) );
  CIN_ASSERT( T , bound_T , bound_T );
  CIN_ASSERT( LA , N , 2 * N );
  CIN_ASSERT( LB , 4 , bound_LB );
  vector<vector<int>> e( N );
  REPEAT( M ){
    CIN( int , u , v );
    e[u].push_back( v );
    e[v].push_back( u );
  }
  CIN_A( int , 1 , T , target );
  CIN_A( T2<int> , 0 , N , xy );

  vector<int> hind;
  auto edge = [&]( const int& u ){
    vector<pair<int,bool>> answer{};
    RUN( e[u] , v ){
      answer.push_back( { v , hind[v] == 0 } );
    }
    return answer;
  };
  Graph graph{ N , edge };
  ZeroOneBreadthFirstSearch bfs{ graph , -1 };

  // O(N+M)
  auto Path = [&]( const int& t ){
    // O(N)
    bfs.Initialise( target[t] );
    // O(M)
    // (!)現時点での信号の状況しか考慮せずに最短径路探索
    while( bfs.Next() != target[t+1] ){}
    vector<int> path{ target[t+1] };
    // O(N)
    while( true ){
      auto& u = bfs.prev( path.back() );
      if( u == target[t] ){
	break;
      }
      path.push_back( u );
    }
    return path;
  };

  // O(N)
  vector<int> A{};
  vector<vector<int>> A_inv( N );
  vector<int> B{};
  vector<T2<int>> line( N );
  auto InitialiseArray = [&](){
    if( A.size() == 0 ){
      A.resize( LA );
    }
    int c_x = GetRand( -10 , 10 );
    int c_y = GetRand( -10 , 10 );
    FOR( i , 0 , N ){
      auto& [x,y] = xy[i];
      line[i] = { c_x * x + c_y * y , i };
    }
    Sort( line );
    FOR( i , 0 , N ){
      A_inv[A[i] = line[i].second] = { i };
    }
    FOR( i , N , LA ){
      A_inv[A[i] = GetRand( 0 , N - 1 )].push_back( i );
    }
    B = vector<int>( LB , -1 );
    hind = vector<int>( N );
  };

  auto UpdateB = [&]( const int& L , const int& i , const int& j , vector<vector<int>>& query ){
    query.push_back( { L , i , j } );
    FOR( l , 0 , L ){
      if( B[j+l] != -1 ){
	hind[B[j+l]]--;
      }
      hind[B[j+l] = A[i+l]]++;
    }
  };

  auto FillB = [&]( const int& v , vector<vector<int>>& query ){
    auto begin = A_inv[v].begin() , itr = --A_inv[v].end();
    int i = *itr , j = 0 , L = LB;
    while( i + L > LA ){
      if( itr != begin ){
	i = *--itr;
      } else {
	i = LA - L;
      }
    }
    UpdateB( L , i , j , query );
  };

  auto OptimiseB = [&]( const int& v , const int& path_size , const vector<int>& path , vector<vector<int>>& query , Set<int>& vertex ){
    int i_opt = -1 , j = 0 , L_opt = 1 , hit_opt = -1;
    RUN( A_inv[v] , i ){
      int L_max = min( 4 , LA - i ) , hit = 0;
      FOREQ( L , 1 , L_max ){
	hit += ( L == 1 || path[path_size - ( L - 1 )] == A[i] ? 1 : 0 ) - vertex.count( B[L-1] );
	if( hit_opt < hit ){
	  i_opt = i;
	  L_opt = L;
	  hit_opt = hit;
	}
      }
    }
    UpdateB( L_opt , i_opt , j , query );
  };
  
  auto SetOperation = [&]( int& path_size , vector<int>& path , int& count , vector<vector<int>>& query , Set<int>& vertex ){
    // (!)次の頂点しか考慮せずに信号操作
    int v = path.back(); path.pop_back(); path_size--;
    if( hind[v] == 0 ){
      count++;
      // (!)A_inv[v]の末尾に固定
      if( B[0] == -1 ){
	FillB( v , query );
      } else {
	OptimiseB( v , path_size , path , query , vertex );
      }
    }
    query.push_back( { v } );
  };

  // O(T(N+M))
  auto SimulateTavel = [&](){
    int count = 0;
    vector<vector<int>> query{};
    // O(T(N+M))
    FOR( t , 0 , T ){
      // O(N)
      auto path = Path( t );
      Set<int> vertex{};
      RUN( path , v ){
	vertex.insert( v );
      }
      int path_size = path.size();
      while( path_size > 0 ){
	SetOperation( path_size , path , count , query , vertex );
      }
    }
    return pair<int,vector<vector<int>>>{ count , move( query ) };
  };
  
  int repetition = 0;
  vector<int> A_opt{};
  int count_min = 1e5;
  vector<vector<int>> query_opt{};
  while( CHECK_WATCH( 3000 ) ){
    // O(N)
    InitialiseArray();
    // O(T(N+M)), T(N+M) <= 1440000
    auto [count,query] = SimulateTavel();
    repetition++;
    if( count_min > count ){
      A_opt = move( A ); A.clear();
      count_min = count;
      query_opt = move( query );
      COUT( "#trial" , repetition , ":" , count );
    }
  }
  COUT( "#trial count:" , repetition );
  // O(N)
  COUT( A_opt );
  // O(TN), TN <= 360000
  RUN( query_opt , q ){
    COUT( q.size() == 1 ? 'm' : 's' , q );
  }
}

結果はAC！　やっと$2$度目のACです。実行時間も$2926$[ms]で問題なさそう。

点数は$7,322,520,073$で、現時点の順位は267/569位です。周りを見ると提出数が少ない人ばかり。多くの人のスタートラインにようやく着いたというところでしょうか？

何にせよACが取れたので、やっとデバッグパートから改良パートに移れます。嬉しいですね。

しかもビジュアライザが軽くなってきました。なるほど、ビジュアライザがフリーズしてしまったのは出力数が多すぎたからですね。

$2$回目の提出

現在は１つのループで

射影の乱択$O(1)$
射影による$A$の先頭$N$項の決定$O(N \log N)$
$A$の残りの成分の乱択$O(L_A)$
$2$スタンプ間の最短経路を、始端スタンプに到達時点でのON/OFFの情報のみから01BFSで計算$O(T(N+M))$
その最短経路に沿って移動する上で、ON/OFF切り替え時の連続部分列を貪欲に計算$O(T)$ という処理を行っています。

射影による$A$の構成は「（ユークリッド距離で）近い頂点を$A$の近い位置に写す」という利点がありますが、遠い頂点が$A$の中で近くなることはあります。再帰的な平面の$4$分割で「$A$の近い位置に移る頂点は元々近くにある」という方向に調整したほうが良いのかな？

それだと近い頂点が$A$の近い位置に移るとは限らない点が心配ですが、とりあえず提出してみて「近い頂点を$A$の位置に写すこと」と「遠い頂点を$A$の遠い位置に写すこと」のどちらの寄与が大きいかを見てみましょう。

  auto InitialiseArray = [&](){
    if( A.size() == 0 ){
      A.resize( LA );
    }
    int c_x = GetRand( -10 , 10 );
    int c_y = GetRand( -10 , 10 );
    FOR( i , 0 , N ){
      auto& [x,y] = xy[i];
      line[i] = { c_x * x + c_y * y , i };
    }
    Sort( line );
    FOR( i , 0 , N ){
      A_inv[A[i] = line[i].second] = { i };
    }
    FOR( i , N , LA ){
      A_inv[A[i] = GetRand( 0 , N - 1 )].push_back( i );
    }

を

  auto InitialiseArray = [&](){
    A = PlainSort( xy , T2<int>{ 500 , 500 } , 500 );
    FOR( i , 0 , N ){
      A_inv[A[i]] = { i };
    }
    A.resize( LA );
    FOR( i , N , LA ){
      A_inv[A[i] = A[GetRand( 0 , N - 1 )]].push_back( i );
    }

に変更して平面をソートするライブラリ追加です。

点数は$7,282,319,472$で微減しました。射影の方が点数高いようなので、「近い頂点を$A$の位置に写すこと」の方が「遠い頂点を$A$の遠い位置に写すこと」より重要そうです。

$3$回目の提出

平面の再帰的分割はやめて射影に戻すとして、もっと大幅な改良がしたいところです。例えばうまいことループ回数を増やして良い射影が得られないでしょうか？　今日の$2$回目の提出ではビジュアライザのサンプルでのループ回数が$18$回、他の提出でも$40$回程度と心許ないです。

そのためには$1$ループあたりの計算量を減らす必要があり、今のところループ内で行っている処理のうち最も計算量が重いのは01BFSですね。

ということで少し戦略を変えて

まず$2$スタンプ間の最短経路をBFSで（ON/OFF関係なく）前計算する。
各ループではその経路を通ることを決め打つ。（経路を決めるのでスタンプの位置は無視する）
前までは$2$スタンプ間の道中にある頂点を参考にON/OFF切り替え時の連続部分列の取り方を貪欲に選んでいたが、スタンプの位置を無視するので代わりに現在位置から経路上一定距離（適当に決め打つ）の頂点を参考に貪欲に選ぶ。

という高速化をしてみます。各ループの質は下がりますが、その分経路長の総和を$L$とすると$1$ループの計算量が$O(T+N+M+L)$に落ちるので、若干ループ回数が上がると思います。

経路の決め方を一新するので実装は大幅に変わります。大変ですね。ひたすらバグらせまくって実装大苦戦しましたが、ビジュアライザのサンプルループ回数が$411$回に増え、ON/OFF切り替え回数も$5859$回に減りました。

点数は$7,277,780,972$の微減で、現時点の順位は323/647位です。順位が一気に落ちてしまいました。

まあ今回の狙いはループ回数の確保だったので良しとします。$411$回もループできるなら射影の乱択以外にも色々試せますので。

$4$回目の提出

あとよく考えたら点数って相対スコアなんですね。絶対スコア（小さいほど良い）はむしろ$321732$から$315816$に良くなっていたので、相対スコアの増減を気にしても意味なかったです。ここからは絶対スコアを気にしていきます。

とりあえず$3$回目の提出をビジュライザで観察してみると、ON/OFF切り替え時の連続部分列の長さが$2$で取れていることが多く、きちんと貪欲法が機能してそうです。一方で長さが$3$に取れることは稀で、$4$以上となるとめったにないようです。

貪欲法の評価式を多少いじってみると何か良いことあるかも？　例えば連続部分列が長いほど評価が高いようにいじってみます。

	  if( hit_opt < hit ){
	    L_opt = L;
	    i_opt = hitA[L].second;
	    hit_opt = hit;
	  }

を

	  if( hit_opt <= hit ){
	    L_opt = L;
	    i_opt = hitA[L].second;
	    hit_opt = hit;
	  }

に変えるだけなので楽ですね。また$3$回目の提出では

連続部分列の長さの上限$8$
貪欲法で確認する範囲の上限$8$

を決め打っていました。前者は$L_B$が大きい場合もループ回数を増やすため、後者は現在位置から経路上で遠い位置の頂点の寄与を減らすためです。$L_B = 5$の場合のループ回数に余裕があるので連続部分列の長さの上限を$12$程度に上げ、また貪欲法で確認する範囲の上限$8$を$[8,24]$の範囲で乱択することにしてみます。

これで効果があったら、単に貪欲法で確認する範囲の上限を設定する（寄与を$0,1$にする）のではなく寄与を距離に関する連続値にするのも良さそうですね。

ビジュアライザのサンプルではON/OFF切り替え回数が$5860$回と微増ですが、きちんと連続部分列が長さ$5$まで選択されています。

提出したらRE。ほとんどいじっていないのに何で？

$5$回目の提出

どうやら$3$回目の提出の時点でうっかり連続部分列の長さの上限$8$と貪欲法で確認する範囲の上限$8$を混同したコードを書いてしまっていたため、これらの変更時に配列外参照が起こってしまっていたようです。

    if( num + L_bound < path_size ){
      next_occur[path[num + L_bound]]++;
    }

を

    if( num + sight < path_size ){
      next_occur[path[num + sight]]++;
    }

に修正です。これでやっと治りました。

このデバッグもかなり苦戦しました。というのも普段は小さい入力数に特化したデバッグモードを時間強に要しているのですが、スコアコンは入力数が多いのでデバッグモードで実行すると余計な出力が出すぎてさっぱりになってしまいます。

デバッグモードでの出力はせずに、サンプルをseed0からseed1に変えてabortとgdbを駆使しての愚直なデバッグでやっと原因特定できました。というわけで気を取り直して再提出。

絶対スコアが$315816$から$252330$へ大幅な改善。相対スコアも$8,784,489,143$に上がりました。ただ順位は295/651位と下がったまま。他の参加者の改善ペースより遅いということですね。

$6$回目の提出

ビジュアライザのサンプルseed1を見てみると、$L_B = 11$で大きめですがループ回数は$173$回と十分ループできている一方、最適回数の更新は$5$回目のループで止まってしまっています。

現状各ループで行っているのは

射影を乱択
$A$の先頭$N$項を射影で計算
$A$の残りの項を乱択
貪欲法で考慮する経路上の頂点の距離は$[8,24]$の範囲を乱択
前計算した経路に沿って移動しつつ、移動の直前に毎回ON/OFF切り替えを貪欲に計算

というものです。絶対スコアが大幅に改善したので、予定通り貪欲法で実質$0,1$値の寄与を考えている部分を連続値にしてみようと思います。つまり、現在の頂点から経路上で近ければ近いほど寄与を重く考えるようにしてみます。

これで遠い頂点の寄与を考慮しすぎることはなくなるので、経路上の距離$24$より遠い頂点まで考慮できます。試しに距離$64$まで考慮することにしました。

ビジュアライザのサンプルseed0のループ回数が$303$回に減りましたが、ON/OFF切り替え回数は$5366$回に減りました。これは期待できそうです。

しかし提出してみると絶対スコアが$252330$から$252685$に微増してしまいました。

$7$回目の提出

ビジュアライザのサンプルseed0（$L_A = 612, L_B = 5$）以外を確認して悪化の原因を探ってみます。

seed1（$L_A = 1099, L_B = 11$）だと、今日の$5$回目の提出はループ回数$187$でON/OFF切り替え回数$5890$、一方で今日の$6$回目の提出はループ回数$144$でON/OFF切り替え回数$5999$と悪化。
seed2（$L_A = 682, L_B = 20$）だと、今日の$5$回目の提出はループ回数$123$でON/OFF切り替え回数$5567$、一方で今日の$6$回目の提出はループ回数$107$でON/OFF切り替え回数$5474$と改善。
seed3（$L_A = 1024, L_B = 7$）だと、今日の$5$回目の提出はループ回数$240$でON/OFF切り替え回数$6456$、一方で今日の$6$回目の提出はループ回数$182$でON/OFF切り替え回数$6751$と悪化。

$L_B$の大きさはあまり関係なさそうで、$L_A$が大きい時に悪化している感がありますね。ループ回数は常に減っていますが、$L_A$が大きい方が減りも大きいせいかな？　じゃあループ回数を担保するために、貪欲法で連続寄与を考慮する長さ$64$を$32$に減らしてみます。

seed0でのループ回数$352$、ON/OFF切り替え回数$5339$で更に改善。
seed1でのループ回数$159$、ON/OFF切り替え回数$6019$で更に悪化。
seed2でのループ回数$144$、ON/OFF切り替え回数$5430$で更に改善。
seed3でのループ回数$210$、ON/OFF切り替え回数$6654$で両者の中間。

何とも微妙な結果ですね。$L_A$が大きい時は近くの頂点の寄与をもっと高くしたほうがいいのかな。あ、そもそも$L_A$が大きい時は$A$の$N$項目以降が乱択に手抜いている部分が大きく効くから、そこを先に直そう。

具体的には、$A$の最初の$N$項と残りでそれぞれ別の射影を引いてみるのが良さそう。

射影$2$本を乱択

やってみました。

seed0でのループ回数$343$、ON/OFF切り替え回数$5296$で更に改善。
seed1でのループ回数$150$、ON/OFF切り替え回数$6053$で更に悪化。
seed2でのループ回数$113$、ON/OFF切り替え回数$5142$で更に改善。
seed3でのループ回数$199$、ON/OFF切り替え回数$6601$でまだ両者の中間。

$L_A$が大きいケースがうまくいきませんね。今は貪欲法での頂点の寄与を、経路上で遠いほど指数関数的減少していくように設定していますが、元はここが$24$まで$1$、残りが$0$という特性関数による離散値だったわけです。

指数関数の代わりに特性関数の軟化を行ったほうが良いかもしれません。例えば正規分布辺りが良さそう？

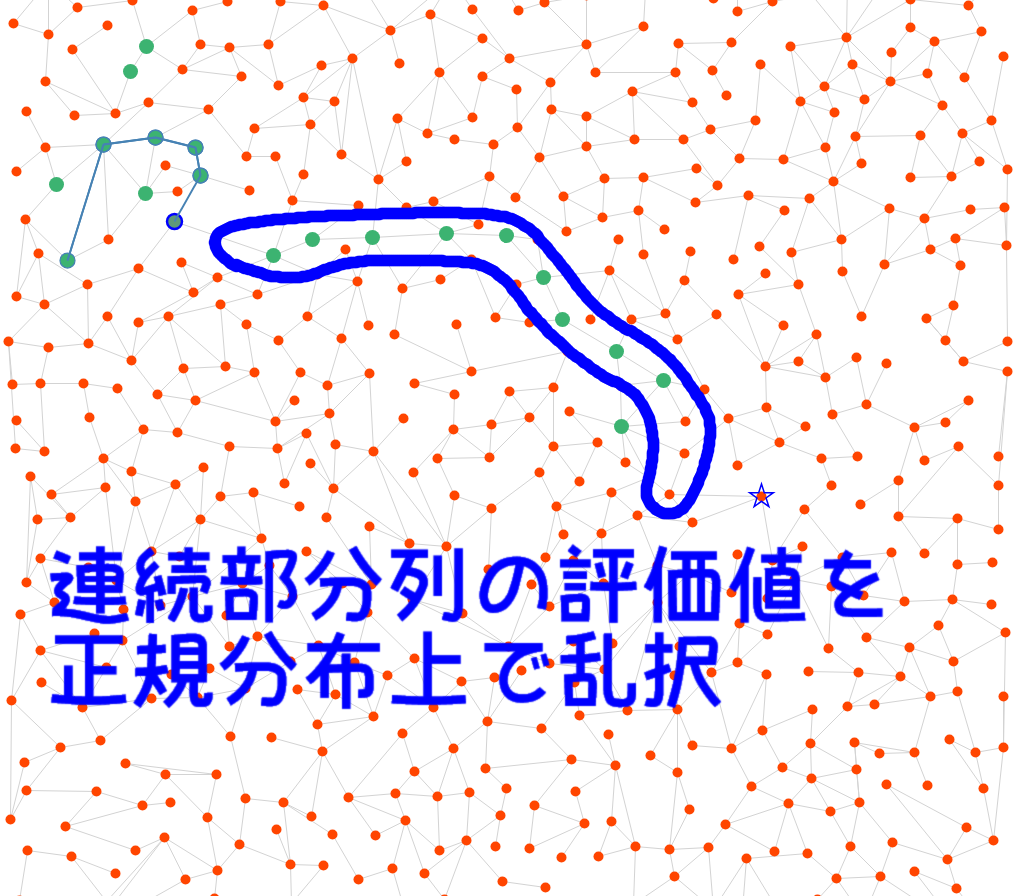
正規分布を乱択

とりあえず実験。

seed0でのループ回数$341$、ON/OFF切り替え回数$5320$でさっきよりは悪化だがまだ改善側。
seed1でのループ回数$150$、ON/OFF切り替え回数$5858$でやっと改善！
seed2でのループ回数$113$、ON/OFF切り替え回数$5065$で更に改善。
seed3でのループ回数$198$、ON/OFF切り替え回数$6607$でまだ両者の中間。

割りと良さそうです。ここいらで提出してみましょう。

結果は絶対スコア$244909$、これまでで一番良い値です。しかし相対スコアは$8,891,380,485$、順位は297/667位。全然上がりませんねえ。

$8$回目の提出。

そろそろループ回数を上げて乱択に頼る戦略を脱却したほうが良さそうです。現在乱択しているのは

$A$の先頭$N$項を決めるための射影
$A$の残りの項を決めるための射影
貪欲法を行うための評価関数に用いる正規分布から取っているサンプル点群の乱択

の$3$つです。射影$1$つなら$1$時限的なので乱択で良さそうですが、$2$つの射影の組み合わせを別個に乱択すると$(\textrm{S}^1)^2$上の乱択となりループ数が足りなくてよくなさそうですね。また正規分布のサンプル点群も、せっかく可微分分布を取っているのですから乱択するよりは摂動させるほうが良さそうです。この辺をどちらか改善していきましょう。簡単そうな射影$2$本からかな。

正規分布のサンプル点群の取り方を一旦固定してON/OFF切り替え回数を$(\textrm{S}^1)^2$上の可微分関数$f$の離散化だと思うと、$f$は$\mathbb{R}^2$上の可微分周期関数$\overline{f}$を定めるので方程式$\nabla \overline{f} = 0$を考えればよく、そう、ええと……なるほど、よし、完璧だ……。

ついでに$L_A$が$N +10 = 610$以下の時はループ回数を増やすことを目指して射影を$1$本だけにして、$A$の$N$項目以降は適当にグラフ上をランダムウォークさせます。

seed0（$L_A = 612, L_B = 5$）でのループ回数$345$、ON/OFF切り替え回数$5272$で改善。
seed1（$L_A = 1099, L_B = 11$）でのループ回数$154$、ON/OFF切り替え回数$5956$で悪化。
seed2（$L_A = 682, L_B = 20$）でのループ回数$115$、ON/OFF切り替え回数$5071$でやや悪化。
seed3（$L_A = 1024, L_B = 7$）でのループ回数$197$、ON/OFF切り替え回数$6523$で改善。

微妙に悪化しているところもありますが、とりあえず提出。

結果は絶対スコアが$245396$でやや悪化。残念。

$4$日目（8/26月）

今日はほとんど挑戦できません。時間の細かな合間に実装と考察を進めていきますが、コンパイラの入っていないタブレットでコードテストを駆使して（出力が打ち切られるのでビジュアライザが使えない環境で）の実装となるのでバグリやすいです。

というわけで大きな変更は避け、細かい変更をすることにしました。

$1$回目の提出

具体的には、現在同時に乱択している

$A$の先頭$N$項を決めるための射影
$A$の残りの項を決めるための射影
貪欲法を行うための評価関数に用いる正規分布から取っているサンプル点群の乱択

を同時に乱択するのをやめ、上から順に決定していくことで精度が上がるか確認してみました。

また、ループ回数を増やすために各ループの処理を若干高速化させました。入力生成方法にシードがあるということはランダムグラフっぽいので、最悪ケースはあまり気にする必要がなく座標圧縮が有効そうです。

隙を見てコードテストに投げてデバッグし、いざ提出するもWA×50。何で？

あとclarが返ってきました。9時間かけても録画できなかったビジュアライザは単に不具合だったようです。

しかしビジュアライザが録画できるようになったとはいえ、録画結果は紙芝居のような飛び飛びの動画になってしまっており役に立ちませんでした……ビジュアライザの画像をこちらに貼っていないのもそのためです。

$2$回目の提出

ようやくコンパイラのある環境に戻って出力結果をビジュアライザに投げられるようになったのでデバッグ。出力形式間違ってました。そこを直して再提出しようとしましたが寝落ち。

$5$日目（8/27火）

今日も時間があまり取れないので、細かな改良を主に。

$1$回目の提出

昨日の直しのついでにassertとデバッグ用コメントを増やして意図通りの挙動になっているかの確認をしました。すると色々バグが見つかったので修正して、提出。

絶対スコアが昨日のベストの$244909$から$241974$に改善しました。射影$2$本の同時乱択より$1$本ずつ順番に乱択した方が良くなったことになります。

なるほどね、実行時間制限が$3$[s]だとstrictな最適化である同時推定より不完全な最適化である$2$段階推定の方が収束が早いというわけですか。これは何かのヒントかもしれません。……もしかして残る正規分布のサンプル点群の推定も？

$2$回目の提出

貪欲法の評価関数に用いている正規分布のサンプル点群の乱択を一気にするのをやめて、正規分布のスケールと$1$点目と$2$点目と……$32$点目を順に乱択していくことにしました。

ビジュアライザが使えないのでただ祈るのみですが、とりあえず提出です。

絶対スコアは$241974$から$236771$に改善しましたが、順位は387/804位です。全然変わりませんね！

しかも周りは$1$・$2$回目の提出の人ばかり。何だか恥ずかしくなってきました。

$3$回目の提出

コードテストをしてみて思ったのが、

本来は正規分布上を単調に取る予定の点群が、うっかりそうなっていなかった。しかもそうなっていない時に評価値が更新されてしまった。
自分の環境での実行速度よりコードテスト上での実行速度のほうが$10$倍くらい早い気がする。
$1$本目の射影の乱択でON/OFFの切り替え回数はかなり早く収束し、$2$本目の射影の乱択でON/OFF切り替え回数が減ることは$L_A$が小さいとあまりない。

の$3$点です。

1についてふと気付いたのですが、正規分布から点群を取って作る評価関数では次の頂点がONになる保証がありません。点群を単調に取りさえすればランダムグラフならあまり気にしなくても良さそうな気がしますが、最終的なテストケースはいっぱいなのでちょっと気にしたほうが良さそう？

2については、自分の感強だとループ回数が少なさ過ぎて検討してなかった手段も再考の余地がありそうです。特に、連続部分列の長さ上限$L_{\textrm{bound}}$を$\min {12,L_B}$に設定していたわけですが、計算量への$L_{\textrm{bound}}$の寄与は$2$乗オーダーなので、上限は$L_B$でも良さそう。

3については、射影の乱択にかける時間をもっと調整してみようと思います。

とここでまたコンパイルできる環境に戻ったので、ビジュアライザのサンプルで試してみます。

seed0（$L_A = 612, L_B = 5$）でのループ回数$428$、ON/OFF切り替え回数$5194$。
seed1（$L_A = 1099, L_B = 11$）でのループ回数$172$、ON/OFF切り替え回数$5502$。
seed2（$L_A = 682, L_B = 20$）でのループ回数$104$、ON/OFF切り替え回数$4925$。
seed3（$L_A = 1024, L_B = 7$）でのループ回数$233$、ON/OFF切り替え回数$6350$。

全体的に前より改善していますね。seed2での動きを見てみましょう。

これは$1$つ目の射影が縦方向を潰すパターンですね。横方向の距離を無視するので、縦に移動する際は横にONの頂点がズラッと並びます。

何故か$B$に$0$が現れて留まっていることが多いですね。何でだろ？

とりあえず正規分布の$1$点目の修正するのと、$L_{\textrm{bound}}$を変えるのと、射影の時間配分をいじるのと、その他のバグを修正して再提出。

結果はAC×31、RE×19でした。何で？

$4$回目の提出

正規分布から選ぶ点群の$1$点目を調整したらオーバーフローしてた！

直して提出したら絶対スコアが$243867$に悪化しました。正規分布の$1$個目の点を修正したことが原因だとすると、貪欲法の重み付けが結構重要そうです。

正規分布の$1$点目の修正はACとなるケースに影響を与えないはずなので、$L_{\textrm{bound}}$の変更と射影の時間配分の変更のどちらかが原因かな？

$5$回目の提出

射影の時間配分を直して再提出したところ、$242381$点と若干の回復。まだまだ$2$回目の提出に及びません。ということは$L_{\textrm{bound}}$の変更がよくなかったのでしょうね。

次の提出まで$30$分あるので、寝落ちするまえにローカル環境を整えておきます。提出せずともたくさんのケースでスコアを計算できるようにしましょう。

この前ビジュアライザがフリーズした時に試したWindows用のコンパイル済みバイナリにはサンプルがたくさん入っていたので、それを活用します。捨てたので再ダウンロードですが。

今までは

IN VO Solve()
{
  /* 定義本体 */
}

となっていたところを

#ifdef LOCAL
  #define INPUT( T , X , Y ) T X , Y; ifs >> X >> Y;
  #define INPUT_ASSERT( X , ... ) int X; ifs >> X
  #define INPUT_A( T , I , N , A ) vector<T> A( I + N ); FOR( i , 0 , N ){ ifs >> A[i]; }
  #define OUTPUT ofs
#else
  #define INPUT( T , X , Y ) CIN( T , X , Y )
  #define INPUT_ASSERT( X , ... ) CIN_ASSERT( X , __VA_ARGS__ )
  #define INPUT_A( T , I , N , A ) CIN_A( T , I , N , A )
  #define OUTPUT cout
#endif

IN VO Solve()
{

  #ifdef LOCAL
    cout << "ローカルモードで実行します。" << endl;
    int count_sum = 0;
    ofstream ofs{ "a.txt" , ios::trunc };
    FOR( sample_num , 0 , 50 ){
      ifstream ifs{ "C:/Users/user/Desktop/in/" + to_string( 10000 + sample_num ).substr( 1 ) + ".txt" , ios::in };
  #else
    CEXPR( int , bound_N , 600 );
    CEXPR( int , bound_T , 600 );
    CEXPR( int , bound_LB , 24 );
  #endif

  /* 定義本体 */

  #ifdef LOCAL
      count_sum += count;
      cout << sample_num << ": " << count << endl;
    }
    cout << "total: " << count_sum << endl;
  #endif
}

としてローカル環境でのみサンプル50個の総得点を計算するコードになりました。

とっくに提出制限の$30$[m]過ぎていたので、$L_{\textrm{bound}}$を元に戻して再提出。

結果はWA×50です。入出力を書き換えた結果、改行し忘れました。。

$6$回目の提出

早速Windows用コンパイル済みバイナリに同梱されていた$100$ケースの家$50$ケースの絶対スコアを計算していきます。

サンプルの$L_{\textrm{bound}}$書き換え後の絶対スコアは$277815$であるのに対し、サンプルの$L_{\textrm{bound}}$書き換え前の絶対スコアは$278673$……あれ悪化してる。

え、じゃあ原因は正規分布？　$1$点目を修正したらサンプルの絶対スコアが$270550$点に改善。何で？

$6$日目（8/28水）

今週はとても疲れています。。長期コンが来週だったらなあ。

$1$回目の提出

そういえば昨日の$3$回目の提出をビジュアライザで確認した時に$B$に$0$が現れて留まっていることが多かったことが気になりました。

またコンパイラもなくビジュアライザが使えない環境に来ているので、ひたすらソースコードを眺めます。

貪欲法の評価関数がバグっていて、$0$をめちゃくちゃ選びやすくなっていたようなので、正規分布は$3$回目の提出（テストケースが多いとバグる可能性あり）に戻した上で$0$のバグを直しただけの提出。

提出結果は、絶対スコアが$225079$に改善しました。バグ直ってよかった！　順位は確認する時間がありませんでした。

$2$回目の提出

よく考えたら、現在位置から遠い点の寄与を減らすために正規分布を使っていたわけですが、一方で現在位置からON/OFF切り替え$1$回で到達できる点は遠ければ遠い程よいので、正規分布を単純に使うのは悪手っぽいです。

経路上でのONの連結成分の長さが重要な気がするので、貪欲法の評価関数に現在位置の経路上における連結成分の右端座標を考慮させます。

尺取り法とmapによる区間管理で結構重い実装。コンパイラなしの状況ではひたすら実装を進めコンパイラありの環境に戻った後で一気にデバッグしました。

サンプル$50$個の絶対スコアは$238573$に大躍進。これは良さそう。いざ提出！

……結果はAC×29、TLE×21でした！

手元でサンプル回すだけだとTLE検出できなくてよくないですね！

$3$回目の提出

尺取り法＋区間管理で計算量が一気に上がってしまったので、ループ回数は手元だと$1$桁台に落ち込んでいます。恐らくAtCoder環境でも$1$ループが$100$[ms]超えてしまうケースが出たのでしょう。$2$日目の経験を活かして、ループの平均速度を計測しつつ打ち切り時間を計測することにします。

今度はコードテストでしっかりと確認をし、再提出。

結果は絶対スコアが$212621$で改善！　でも順位は427/867位……どんどん落ちていきますねええええ！！！

当面の目標は絶対スコア$200000$の壁を突破することですね。射影の乱択がまだ愚直な感じがするので、平面グラフをうまく変形させたりして何とかならないかな？

イマジナリーShirotsumeさん「いつか、何かで$200000$を打ち破るだろう。だがそれは今日ではないし、射影によってでもない」

そんな……。

$7$日目（8/29木）

乱択しかヒューリスティックに役立ちそうなテクニックを知らないのに、手元の環境だとループ回数が$1$桁しか稼げなかったりしているのではどうしようもありません。

これじゃ乱択どころか整択です。何とかループ回数を稼ぎましょう。

$1$回目の提出

今は長さ$L$ごとに$B$の連続部分列貪欲に決定してから対応する$A$の連続部分列を貪欲に決定しているせいで、計算量に$L_{\textrm{bound}}$の寄与が$2$乗で掛かっています。

そこで、長さ$L$の候補を$B$の決定時点で枝狩りしてしまうことにします。ごっそり減らしたのでこれでループ回数が稼げるはず！

提出結果は絶対スコア$228319$で悪化。何で？

$2$回目の提出

コードテストに投げてみると、ループ回数はきちんと$3$桁台出ています。今回の枝刈りは十分良い枝を残している想定だったので、どこかで意図通りでない実装ミスをしてそうです。

コードとにらめっこした結果、「$B$から除く集合の評価点の最小化」をしていたわけですが、その値を「$B$に残る集合の評価点の最大化」と混同して使ってしまっていました。そこを直して再提出です。

提出結果は絶対スコア$234712$で更に悪化。何で？

$3$回目の提出

空き時間にひたすらコードとにらめっこ。今度は「$B$から除く集合の評価点が$0$」とすべきところを「$B$に残る集合の評価点が$0$」としてしまっていました。$2$回目の提出の修正が中途半端だったようです。そこを直して再提出。

提出結果は絶対スコア$211030$でようやく改善。

$4$回目の提出

ここでコンパイラのある環境に戻ってきました！　サンプルで絶対スコアが確認できます。

そこで、そろそろ抜本的な改善がしたいです。そこで、思い切って射影$2$本の乱択による$A$の決定をやめてみることにしました。

例えば経路に沿って$A$に埋めていくのはどうでしょう？　ただし重複は程々に取り除かないと$A$が網羅的でなくなってスタンプラリーが成功しません。

どうせ経路に沿って埋めるなら、経路を決めるのと$A$を埋めるのを相互に行うのが良さそう。それなら$A$の埋め方を参照して辺の重みを調整して、BFSじゃなくてダイクストラを使ってみましょう。

$A$の決定に乱択がいらなくなるおかげでループ回数も有効に使えます。サンプルを試してみると絶対スコア$163921$と今までにない値！　意気揚々と提出です。

提出結果はWA×8、RE×52でした。何で？

$5$回目の提出

コンパイラがあればgdbでデバッグできて簡単ですね。経路の最初の$0$の扱いをミスってました。

そしてダイクストラで計算した経路たちを繋ぎ合わせる時に端点を二重に繋いでしまっていました。

あとサンプル実行のために追加してたローカル環境用のマクロもミスってました。ミスいっぱいですね。

#ifdef DEBUG
  #define INPUT( T , X , Y ) T X , Y; ifs >> X >> Y;
  #define INPUT_ASSERT( X , ... ) int X; ifs >> X
  #define INPUT_A( T , I , N , A ) vector<T> A( I + N ); FOR( i , 0 , N ){ ifs >> A[i]; }
  #define OUTPUT ofs
#else
/* 省略*/
  vector<bool> appear( N ); appear[0] = true;
  AbstractDijkstra<int,decltype(graph),int,AdditiveMonoid<int>> dijk{ graph , AdditiveMonoid<int>() , int(1e6) };
  FOR( t , 0 , T ){
    // O((N+M)log N)
    auto [w,p] = dijk.GetPath( target[t] , target[t+1] );
    // O(N*L_bound)

を

#ifdef DEBUG
  #define INPUT( T , X , Y ) T X , Y; ifs >> X >> Y;
  #define INPUT_ASSERT( X , ... ) int X; ifs >> X
  #define INPUT_A( T , I , N , A ) vector<T> A( I + N ); FOR( i , 0 , N ){ ifs >> A[i+I]; }
  #define OUTPUT ofs
#else
/* 省略*/
  vector<bool> appear( N );
  AbstractDijkstra<int,decltype(graph),int,AdditiveMonoid<int>> dijk{ graph , AdditiveMonoid<int>() , int(1e6) };
  FOR( t , 0 , T ){
    // O((N+M)log N)
    auto [w,p] = dijk.GetPath( target[t] , target[t+1] );
    // O(N*L_bound)
    p.pop_front();

に修正です。いざ提出！

提出結果は絶対スコア$123880$でした！　ついに$200000$を切りました！　相対スコアも$15,664,802,345$で初の$10^{10}$超え、順位は316/897位に浮上です！

久々に順位が上がってとても嬉しいです。しかも大幅に方針を変えたばかりなので、まだまだ試せることは多そう。

今まで縦に移動する時に無駄に追従してたON頂点たちも目立たなくなりました。それだけ無駄なくONにできているのだと思います。

$8$日目（8/30金）

今日は丸一日コンパイラのある環境です。ただし夜はゆ～さん主催のyukicoder contest 443があるので、疲れすぎないように気をつけます。

$1$回目の提出

$A$の埋め方を決めたおかげで絶対スコアが大幅に改善したものの、その効果が大きすぎたのか正規分布の乱択パートで貪欲法の評価点の更新がほとんど起こらなくなってしまいました。これではせっかくのループの無駄遣いです。

代わりに経路の決め方と$A$の埋め方を交互に更新していくことでループを消費していこうと思ったのですが、どうも経路の更新も$2$回だけで更新が止まってしまいました。

$A$の決め方が経路に過学習されすぎていて、$A$を固定した時の経路に剛性がある状況ですね。

それでもサンプルを試してみると絶対スコア$100157$と更に改善できています。とりあえず提出してバグがないことを確認してみましょう。

提出結果はAC×49、WA×1でした。何で？

$2$回目の提出

これまでに出たWAの原因（推定）は

ON/OFF切り替え回数と移動回数の合計が上限の$10^5$を超えた。
出力方法を間違えた。

の$2$パターンです。1については、既に絶対スコアがだいぶ良くなっているのであまり気にしなくて良さそうですね。2については、$1$個だけWAになる原因としては考えにくいです。

となると原因はこれら以外。ダイクストラ法で何かミスっているとかでしょうかね。経路の重みの上限を$10^6$に設定しているのが問題？　辺の重みは最大$L_B$に設定していて、経路における辺の本数の合計は$10000$程度のオーダーかなと思っていましたが最悪ケースは$T(N-1) = 359400$本ですね。あ、これはオーバーしちゃう。ということは経路の重みの上限は$L_B T(N-1)+1$に設定し直します。

提出結果はAC×49、WA×1でした。何で？

$3$回目の提出

とりあえずassertを増やしてサンプルを回してみましたが何も引っかかりません。提出してREが出れば原因特定に繋がるのでとりあえず提出しましょう。

提出結果はAC×49、WA×1でした。何で？

$4$回目の提出

幸いなことに、正規分布の乱択部分がほとんど影響を与えていない影響で、実行速度が$10$倍以上異なる時間強とAtCoder環境でも出力結果はほとんど同じはずです。

というわけで、自環境での出力結果を片っ端からビジュアルエディタに投げることで手動ジャッジを行ってみました。

するとseed21でs 0 0 0という出力を発見！　経路計算時の座標圧縮によって$A$が通らない頂点が出てしまうわけですが、経路更新時にその頂点を通る可能性を考慮し忘れていました。修正して再提出。

提出結果の絶対スコアは$90690$点！　とうとう$10^5$を切りました！　相対スコアは$21,311,924,815$点、順位は190/926位と大躍進です。

$5$回目の提出

正規分布部分の乱択がほとんど役に立っていないのでそこをバッサリ切ることが可能です。

となるとある程度時間が掛けられるので、経路を固定した上で$A$を更新していきたいですよね。

現状では経路の最初の方からどんどん$A$に重複しないように埋めていき、最後に$A$の残りの部分を経路に沿って重複を許して埋めていっています。

すると重複しないように埋めていっている部分の最後の方はかなりばらばらになってしまっているので、この辺をうまく並び替えてまとまらせるとよいわけです。

UnionFindで$A$の繋がり状態を動的に管理することで$A$を前から順にクラス分けしていき、それらをクラス順にソートすることで$A$をまとめ直してみることにしました。

UnionFindでソート

と、ここで$1$回目のダイクストラ法で異様に経路の重みが小さくなっていることに気付いたのでgdbデバッグを試みます。しかしラムダ式がgdbと相性悪いことを思い出し、気が重くなりました。gdbの表示がめちゃくちゃになってしまいましたが気合で読解します。まだ書き途中のソートは関係なさそうなので一旦コメントアウト。

$1$回目のダイクストラ法と$2$回目以降のダイクストラ法は前者のみ$A$の同時更新をしているため辺の重みの定義が若干違うのですが、そこで$A$と経路の配列を混同してしまっていたことが原因でした。

これでやっと$2$回目以降のダイクストラ法で経路が正しく更新されていくようになりました。とはいえそれでも$3$回くらいしか更新されないみたいですが。手元で計算したサンプルの絶対スコアは$87335$で一応改善しているので、バグがないことを確認するために念の為提出します。

提出結果は絶対スコアが$77202$に改善、相対スコアは$24,761,816,558$で順位は133/935位に上がりました。嬉しいですね。

$6$回目の提出

経路の更新部分が直せたので、改めてソートを復活させて$A$の更新を試みます。目指すは、$A$の中でばらばらになってしまっている断片をうまくまとめ上げることです。とりあえずは以下の手順を試してみます。

最初は$A$と経路$P$をダイクストラ法の反復で同時に（$A$を使って経路$P$を決めつつ$A$を経路$P$に沿って埋めていく）計算する。$A_{\textrm{next}}$を$A$で初期化する。
UnionFindでソートした$A_{\textrm{next}}$を用いて経路$P_{\textrm{next}}$をダイクストラ法の反復で計算する。
経路$P_{\textrm{next}}$の重みが経路$P$より小さければ、$A$と経路$P$をソート後の$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、経路$P_{\textrm{next}}$を用いて$A_{\textrm{next}}$を定義し直し2に戻る。
$A$と経路$P$を確定させる。

という処理をしています。これらの処理は手元の環境だと$2000$から$3000$[ms]かかるのでサンプルの絶対スコアにあまり意味がありませんが、AtCoder環境だと$300$[ms]程度で終わってくれます。試しに提出してみます。

提出結果の絶対スコアは$76705$で少し改善、相対スコアは$24,886,148,559$で順位も129/937位とわずかに上がりました。

今日はここまで。yukicoderに参加して1完でした……。

$9$日目（8/31土）

今週は土日もややごたごたしているので、もうあまり更新できないかもしれません。大幅な変更を狙うより、細かい変更を重ねていこうと思います。

$1$回目の提出

昨日は$A$の更新と経路の更新を交互に行いましたが、$A$の更新は全順序によるソートではなくクラス分けによるソートをしているため冪等的ではありません。従って、繰り返せば繰り返すほど効果が上がる可能性もあります。

というわけで、経路を変えずに経路の重みが下がるだけソートを繰り返し、下がらなくなったら経路を更新する、という形に直してみます。

手元の環境ではもはやTL以内にほとんど処理できない重さになっているためサンプルの絶対スコアはほとんど変化しなくなってしまっている（恐らく更新の収束までに$10000$[ms]くらい要している）ので、実行結果が良くなっているかどうかはコードテストと実際の提出頼みになります。というわけで情報を増やすためにもなるべく提出していきます。

結果はAC×49、RE×1です。う～ん。実はここ数回の提出用のコードで、手元の環境ではごくまれに何度か実行エラーが出ていました。しかし再現性がなくassertによるものでもないため原因が特定できていません。

$2$回目の提出

ソースコードが長大すぎて目視でのバグ検出が絶望的なので、手元とコードテストでひたすら実行を繰り返すことでデバッグしてみます。再現性がない原因が正規分布の乱択によるものなのか実行時間の不定性によるものなのか切り分けるため、正規分布の計算部分を全てコメントアウト＋念の為abortしておきます。

提出結果はAC×49、RE×1のままです。実行時間は$912$[ms]で、元々経路更新の打ち切り時間に設定していた$1200$[ms]より短いのでバグに再現性がありそうです。

ということはこれまでに出ていた再現性のない実行エラーとは別のものであって、手元のサンプルには引っかからないけれどAtCoderの暫定テストケースには入っているものに引っかかるものがありそう……？　困りましたね。

$3$回目の提出

更に原因の切り分けのため、定義本体のassert（入力受け取りとライブラリー内除く）を全てコメントアウトして提出してみます。

提出結果はAC×49、WA×1です。ビンゴですね。意図通りの挙動かどうかをチェックするためのassertがREの原因で、それを外すとWAになるというわけです。

これまでに出たWAの原因（推定）は

ON/OFF切り替え回数と移動回数の合計が上限の$10^5$を超えた。
出力方法を間違えた。
長さが$0$の部分列を選んだ。

の$3$パターンです。とりあえず疑うべきは3でしょうね。前と同じパターンのミスと信じて該当箇所を確認してみると、やはり同じミスを確認。そこを修正し、コメントアウトしたassertは自環強でのみ機能するように設定し直し、ついでに正規分布の乱択も復活させて提出です。

提出結果はRE×50でした。バグ修正後に自環強で回しただけでコードテストし忘れた！

$4$回目の提出

コードテストに投げると経路と$A$の更新ループ中に実行エラーとなります。自環強ではここのループが$3000$[ms]で$2$回くらいしかできないので実行エラーが出なかったわけですね。

自環境のみ実行時間制限を$10000$[ms]に拡張して再確認です。分かりやすい初期化ミスが見つかったので修正。コードテストに投げてみると、きちんと経路と$A$の更新ループが行われていることが確認できます。

しかし提出結果は昨晩の$76705$点から$79018$点と悪化。残念です。

$5$回目の提出

今日の$4$回目の提出と昨晩の提出と比較してみると、

経路の重みはどちらが小さい時もある。
今日の$4$回目の提出の方が経路の辺の数が小さい。
今日の$4$回目の提出の方が座標圧縮のサイズ（経路中に現れる頂点の種類数）が大きい。
今日の$4$回目の提出の方が経路と$A$の更新回数が多い。
今日の$4$回目の提出の方が経路と$A$の計算に時間がかかっている。
今日の$4$回目の提出の方が正規分布乱択前のスコアが悪い。

6を何とかすべきですが、4と5はあまり関係なさそうです。更新回数が多いのはいいことですし、時間がかかっても残り時間で貪欲法部分の更新はほとんど起こっていません。

となると原因は3かも。座標圧縮のサイズを優先してみましょうか。コードテストで試してみると確かにスコアが上がってそう。座標圧縮すればするほど$A$の中にまとまりを持った部分を作りやすいからでしょうか。

とりあえず提出してみたものの、絶対スコアは$77691$でまだ昨晩に届かず。もう少しコードテストを観察してみます。

$6$回目の提出

今日の$5$回目の提出と昨晩の提出を比較してみると

今日の$5$回目の提出の方が経路の重みが小さい。
今日の$5$回目の提出の方が経路の辺の数が小さい。
座標圧縮のサイズ（経路中に現れる頂点の種類数）はどちらが小さい時もあるが昨晩の方が優勢。
今日の$5$回目の提出の方が経路と$A$の更新回数が多い。
今日の$5$回目の提出の方が経路と$A$の計算に時間がかかっている。
今日の$5$回目の提出の方が正規分布乱択前のスコアが悪い。

という状況です。座標圧縮を優先してもなお昨晩より劣っている理由は、現在回しているループ

$A$を用いたパスの更新
パスを用いた$A$の更新
$A$のソート

のうち2,3は座標圧縮に全く貢献せず、かつパスと$A$の像に対して強く過学習してしまうため、1での更新が生じにくいことだと推測します。

というわけで1を優先的にループするようにしましょう。具体的には現在の

最初は$A$と経路$P$をダイクストラ法の反復で同時に（$A$を使って経路$P$を決めつつ$A$を経路$P$に沿って埋めていく）計算する。$A_{\textrm{next}}$を$A$で初期化する。
UnionFindでソートした$A_{\textrm{next}}$を用いて経路$P_{\textrm{next}}$をダイクストラ法の反復で計算する。
経路$P_{\textrm{next}}$の重みが経路$P$より小さければ、$A$と経路$P$をソート後の$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、経路$P_{\textrm{next}}$を用いて$A_{\textrm{next}}$を定義し直し2に戻る。
$A$と経路$P$を確定させる。

という処理を

最初は$A$と経路$P$をダイクストラ法の反復で同時に（$A$を使って経路$P$を決めつつ$A$を経路$P$に沿って埋めていく）計算する。$A_{\textrm{next}}$を$A$で初期化する。
UnionFindでソートした$A_{\textrm{next}}$を用いて経路$P_{\textrm{next}}$をダイクストラ法の反復で計算する。
経路$P_{\textrm{next}}$の重みが経路$P$より小さければ、$A$と経路$P$をソート後の$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、経路$P_{\textrm{next}}$を用いて$A_{\textrm{next}}$を定義し直し2に戻る。
UnionFindでソートした$A$を用いて経路$P_{\textrm{next}}$をダイクストラ法の反復で計算する。
経路$P_{\textrm{next}}$の重みが経路$P$より小さければ、$A$と経路$P$をソート後の$A$と経路$P_{\textrm{next}}$で置き換え、経路$P_{\textrm{next}}$を用いて$A_{\textrm{next}}$を定義し直し2に戻る。
$A$と経路$P$を確定させる。

という$2$重の処理に変更してみます。

提出結果は絶対スコア$74055$でようやく昨晩より改善！　相対スコアは$25,374,408,201$で順位は131/970位に落ちました。

$7$回目の提出

まだまだやれることは色々ありそうですが、時間が残り限られてきています。とりあえず次の$2$つに絞って行こうかと思います。

正規分布の乱択の改善（高速化のために枝刈りしたけど時間が今は余っているので戻す）
座標圧縮後の部分グラフに対する最小全域木をHL分解して$A$の再計算

1は2の実行時間次第で邪魔になるので、2を頑張りましょうか。

今はダイクストラ法で作った経路に沿って$A$を重複しすぎないように埋めていっていますが、座標圧縮が経路の重み削減より効果的ということは$A$に余裕を持たせられることが実際の移動回数みより大事であるということなので、それなら座標圧縮後の頂点数$-1$本の辺で全体を網羅できるようにKruscal法で最小全域木を取って$A$に埋めるのが良さそうです。

そして$A$がバラバラになりすぎないようにHL分解もしよう、というのが今回の作戦です。Kruscal法もHL分解も未verifyな自作ライブラリで何とかなるでしょうか。実装の苦手な身としては捨て身覚悟の選択です。

当然のようにバグりにバグったので、コメントとassertをめちゃくちゃ増やして頑張りました。

提出結果は絶対スコアが$81804$で悪化！　何で！

$8$回目の提出

コードテストを走らせてみると、座標圧縮のサイズは確かに小さくなっていますが、経路の重みが大きくなったり小さくなったり振動してしまっています。それもそのはず、ソートで$A$を更新するパートは座標圧縮に寄与しますがクラスカル法とHL分解ほどは経路の重みに寄与しないので、それらが繰り返される時に座標圧縮のサイズ以外がフラフラしてしまうからですね。

結果的に$A$と経路を決定後の貪欲法がうまく働きにくくなっているようなので、座標圧縮に注目しつつももう少しクラスカル法とHL分解の強みを残すバランス感で実装し直しました。具体的には

最初は$A$と経路$P$をダイクストラ法の反復で同時に（$A$を使って経路$P$を決めつつ$A$を経路$P$に沿って埋めていく）計算する。
UnionFindでソートした$A$を用いて経路$P_{\textrm{next}}$と$A_{\textrm{next}}$をダイクストラ法の反復で計算する。
$A_{\textrm{next}}$の像のサイズが$A$より小さければ、$A$と経路$P$を$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、像のサイズは$A$と同じで経路の重みが減っているならば経路$P$のみ経路$P_{\textrm{next}}$で置き換え、2へ戻る。
クラスカル法で求めた$A$の最小全域木を$P$の最頻値を根としてHL分解したものを用いて経路$P_{\textrm{next}}$と$A_{\textrm{next}}$をダイクストラ法の反復で計算する。
$A_{\textrm{next}}$の像のサイズが$A$より小さければ、$A$と経路$P$を$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、像のサイズは$A$と同じで経路の重みが減っているならば経路$P$のみ経路$P_{\textrm{next}}$で置き換え、2へ戻る。
$A$と経路$P$を確定させる。

と言った感じです。

提出結果は絶対スコア$73285$でわずかに改善。しかし相対スコアは$25,573,687,382$で、順位は133/990位と更に落ちてしまいました。皆さんの改善ペースにどんどん置いてかれているんでしょうねえ。

$10$日目（9/1日）

そろそろ各ON/OFF切り替えの貪欲法部分の改善に戻ってみたい気もしてきました。今の貪欲法は最初の方から全く変わっておらず、

まず$B$の連続部分列を長さごとに（現在は枝刈りにより長さ$1$と$L_B$のみ）探索して補集合の評価値の高い（取り除いても良い）ものを特定する（元々は尺取り法だけど長さが$1$と$L_B$なら全探索で良くなる）。
次に$A$の連続部分列の長さごとに、上で選んだ$B$の連続部分列を固定した上で評価値の高い$A$の連続部分列を尺取り法とmapによる区間管理で特定する。

という感じです。評価値を与える関数は

経路上の現在位置から$1$回のON/OFF切り替えで到達可能になる点までの辺の本数
経路上の現在位置から離れれば離れるほど小さい値となる関数を正規分布上の点群（$33$次元分）を用いて定めたもの

の$2$つを辞書式順序で組にして与えています。

枝刈り部分はビジュアライザを回してみた結果から考えたもので、当時の経路が基本的にON/OFF切り替え時の連続部分列の長さを$1$か$L_B$のみにしても変化が見られなさそうだったことから採用しました。以前はもう少し増やしていたので、実行時間に余裕が残ればそこを復活させる予定です。

$1$回目の提出

評価関数に正規分布を使っているのは遠くの点を考慮しすぎないように調整する意図です。元々は正規分布でなく$2$値関数を使っていたところを滑らかにしてみた感じで、ここをまずは改良していこうと思います。

正規分布の$33$次元は分散を表す$1$変数とサンプル点群$32$個を表す$32$変数（ただし実行時間に合わせて$26$変数まで減らす）からくるもので、原点から離れたサンプル点群の変化は貪欲法にさほど影響を与えなさそうなので原点に近ければ近いほど多段階推定の集中的な乱択をするようにしていました。

一方で現在のように多段階推定全体を通しても更新がなかったりあってもせいぜい$2$回程度となっている状況では乱択をもっと劇的に行った方が良いと思うので、正規分布とは限らない分布、例えば元々の$2$値関数も含むようにして多段階推定も同時推定に戻してみることにします。

提出結果は絶対スコア$73308$とわずかに悪化。正規分布部分の寄与がほとんどないとはいえ、他の分布よりはマシなようです。というわけでここは元に戻しましょう。

あとrandomの綴りが何箇所かrandamになっていました。ここも修正することで高速化を図ります。

$2$回目の提出

正規分布の乱択部分の調整をしても改善しなかったので、乱択部分の実行時間はあまり気にしなくて良いことが分かりました。

なので、貪欲法の高速化のためにしていた枝刈り（長さを$1$と$L_B$に限定）を少し前の版（$7$日目の$3$回目の提出）に戻してもう少し長さの候補を広げるようにしてみます。尺取り法で長さごとに$B$の連続部分列を選んで、長さと評価値の積順序で極大なものだけを残す感じです。

すると正規分布の乱択部分での更新回数が、ソートやクラスカル法やHL分解を試して以降はほぼ$0$回でせいぜい$2$回になってしまっていたものが$4$回程度に増えてくれました。

長さを$1$と$L_B$にする枝刈りの妥当性は元々ビジュアライザで推定したものですが当時は$A$を$2$本の射影によって乱択していて弱かったせいで、$A$がきちんと強ければ長さも増やした方が更新しやすいんですね。

ヒューリスティックのテクニックは乱択しか持っていないのだから、乱択をとことん突き詰めて考察するのが良さそうですね。

提出結果の絶対スコアは$66358$点に大幅改善！　相対スコアは$28,146,422,393$で、順位は103/1010位！　とうとう100位が近づいてきました！

順位表

今まで周りにちらほらいた黒色がいなくなった！！

$3$回目の提出

$2$回目の提出のビジュアライザを眺めて作戦を練ります。しっかり長さが$1$と$L_B$以外の連続部分列も選択してくれている様子が分かったので気持ち良いです。

今は$A$と経路の更新で用いているダイクストラ法に渡す辺の重みとして、$A$の隣接成分左右$L_B-1$個以内にあるものは重み$1$、そうでないものは$L_B$と定めています。

本来ならば「$B$に登録されている場所へは重み$0$、登録されていない場所は重み$1$」としたいところですがこれを01BFSで処理するには$B$の情報も頂点に追加しなければならないため対応するグラフの頂点数が$N^{L_B+1}$になってしまうのが問題です。

そこで代わりに最初以外は現在位置が$B$に登録されていることに目をつけ、「$B$に$A$の長さ$L_B$の連続部分列が登録されていて現在位置が$B$の端点に対応する場合はON/OFFの切り替え無しで$L_B-1$個先の頂点までいける」という情報を盛り込もうとした結果が今の重みによるダイクストラ法です。

これをもう少し改善して本来の01BFSに近づけていけたら良さそうですね。例えばありえる$B$の情報を完全に頂点に持たせるのではなく、擬似的に$A$の長さ$L_B$の連続部分列が選ばれている状況のみを考えてその情報を頂点に持たせるのはどうでしょう。現在位置は$B$の中にあることを使えば、グラフの頂点数が$(L_A-L_B+1)L_B$、辺の本数が$O((L_A-L_B+1)L_B^2)$で01BFSが可能なサイズです。

ただしかなり重い処理となりそうなので、$A$と経路の更新のループ回数はかなり減るでしょう。うまくいくかなあ。

頑張って実装してみた結果、コードテストに投げると$L_B = 11$の時の01BFS$1$回でおよそ$5000$[ms]掛かってました。悲しい。

まず辺の本数に対する$L_B$の寄与が$L_B^2 \log L_B$乗のオーダーになっているので、01BFSの際は$L_B$の代わりに$4$くらいの定数を使ってみるのがいいかも？　と思ったのですがそれでもおよそ$1000$[ms]かかりました。

よし、諦めよう！

本質的な改善は後回しにして、今のうちに定数倍高速化を仕上げておきます。

具体的には不要になったメモリの開放とかですね。$A$と経路の計算で大量に用意した配列たちは貪欲法パートではゴミとなります。$1$つ$1$つはあまり大きくないですが、念の為削除しておきましょう。

  vector<int> A_next( LA );
  vector<int> A_opt( LA );
  vector<bool> appear( N , true );
  vector<bool> appear_next{};
  vector<bool> appear_opt{};
  vector near( N , vector<bool>( N ) );
  vector<vector<bool>> near_next{};
  vector<vector<bool>> near_opt{};
  vector<int> path_next{};
  vector<vector<int>> class_A{};
  vector<int> cc_Dom_A( cc_size );
  vector<int> cc_Dom_A_inv( LA , -1 );
  vector<vector<T3<int>>> de{};
  vector<T2<int>> de_enum{};

を

clear();

です。配列たちとの楽しかった思い出も徐々に失われていきます。

提出結果は絶対スコア$66358$で全く変わらず。相対スコアは$28,107,883,104$で、順位は110/ 1023位に落ちました。

それはいいのですが、何故か使用メモリが$4644$[KB]から$4764$[KB]に微増しました。何で？

$4$回目の提出

ついでにファイルサイズも削減していきましょう。既に$110181$[Byte]になっていてyukicoder奈良余裕でファイル容量制限オーバーです。今回使わなかった二分探索ライブラリ、尺取り法ライブラリ、合同式ライブラリなどを削除して$94638$[Byte]に改善できました。すっきりしたほうが実行する側にも考察する側にも優しいですからね。

01BFSの案は実を結びませんでしたが、ダイクストラ法を改善したい気持ちは変わりません。

今の重みの決め方だと、連続部分列を短く取って$B$をキープする戦略が取れる状況をうまくカバーできていないからです。実際、ビジュアライザを観察するとちょうどスタンプに到達するタイミングでしばしばそのような経路が選択されているので、そういう動きも考慮した重みの決め方をしたいです。

しかし辺の重みを各ループごとに動かすことはできません。何故なら、$A$と経路の更新では経路の重みを考慮しているため、辺の重みをループごとに変えてしまうと更新が正当化できなくなるからです。

というわけでできることは、なるべく初期値だけで決まる値で辺の重みを決めることです。例えば、スタンプから貼られている辺のみ一律で重み$1$にしてしまうのはどうでしょう？

  auto edge = [&]( const int& i ){
    vector<T2<int>> answer{};
    RUN( e[i] , j ){
      if( appear[j] ){
        answer.push_back( { j , near[i][j] ? 1 : path_length } );
      }
    }
    return answer;
  };
  /*省略*/
      auto [w,p] = dijk.GetPath( target[t] , target[t+1] );

を

  int source_vertex , target_vertex;
  auto edge = [&]( const int& i ){
    vector<T2<int>> answer{};
    RUN( e[i] , j ){
      if( appear[j] ){
        answer.push_back( { j , i == source_vertex || j == target_vertex || near[i][j] ? 1 : path_length } );
      }
    }
    return answer;
  };
  /*省略*/
      auto [w,p] = dijk.GetPath( source_vertex = target[t] , target_vertex = target[t+1] );

に変更です。

提出結果は$67053$点に悪化。しかし手元でサンプルを回したところ、改善しているケースも多々ありました。というかむしろ$50$サンプルの絶対スコアは$79187$から$78664$に改善しています。手元での実行時は処理速度の早いAtCoder環境に結果的なループ回数を近づけるためにTLを$10000$[ms]に引き伸ばしている点で正確ではないですが（本当はもっと近づけるために$30000$[ms]にしたいのですが$50$ケース回すと$25$分掛かってしまい提出間隔に近くなってしまいます）、方向性自体が悪いわけではなさそうです。

$5$回目の提出

残り時間も少ないので、提出による情報収集を遠慮なくしていきましょう。例えば$4$回目の提出でスタンプから出る辺とスタンプに入る辺の重みを変えましたが、スタンプに入る辺のみを変えるというのも試してみたいです。

これは、ビジュアライザでスタンプから出る際に長さ$1$の連続部分列を選択しているのは直前の選択でいい感じの連続部分列を取っていてそこに戻ろうとする時に限られるからです。つまり能動的な選択ではないため、経路の決定段階では考慮しないことにしてみました。

手元のサンプル$50$個の絶対スコアは$79689$にむしろ悪化しましたが、先程は手元とAtCoder環境で改善と悪化が逆転していたので遠慮なく提出します。

提出結果は絶対スコア$68475$で悪化。この方向性はやめておきましょう。

$6$回目の提出

デバッグ出力も少しずつコメントアウトしていきます。そろそろバグも少なくなってきたので。

$A$と経路の評価値更新状況（更新してもしなくてもその結果を出力）
正規分布上の点群の乱択による評価値更新（更新した場合のみその結果を出力）
最終的なパラメータ

のみに絞ってみることで、コードテストによる考察を進めやすくしてみます。

正規分布の乱択は実行時間に応じて$27$変数から$33$変数まで変わりますが、コードテストによると評価値の更新が起こるのは多段階推定の$1$変数目が主で、しかも最初の$5$ループ程度で更新が収束しています。まれに$20$ループ目を過ぎて更新することもあるので、多めに見積もって$30$ループ目で収束している想定をし、時間だけではなくループ数でも$1$変数目の推定を打ち切るようにしてみます。$2$変数目以降に時間を回すことで、更新の可能性を少しでも上げる狙いです。

提出結果は絶対スコア$65951$と僅かに改善！　しかし相対スコアは$27,997,923,260$で、順位は残念ながら$112$位に落ちてしまいました。

$7$回目の提出

順位表で上位のスコアを見ると、相対スコア$40,000,000,000$超えがズラッと並んでます。おかしいですね……みんな正規分布の点群をひたすら乱択しているはずでは……？　何故こんなに差が出るのでしょう？　もしかして正規分布の点群を乱択する以外に、もっといい乱択箇所がある？

この時点での提出回数はCE等も含めると$54$回、もはやソースコードを乱択していると言っても過言ではありません。他にも乱択できそうなところは……そうだ！

今は$A$と経路の更新で

最初は$A$と経路$P$をダイクストラ法の反復で同時に（$A$を使って経路$P$を決めつつ$A$を経路$P$に沿って埋めていく）計算する。
UnionFindでソートした$A$を用いて経路$P_{\textrm{next}}$と$A_{\textrm{next}}$をダイクストラ法の反復で計算する。
$A_{\textrm{next}}$の像のサイズが$A$より小さければ、$A$と経路$P$を$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、像のサイズは$A$と同じで経路の重みが減っているならば経路$P$のみ経路$P_{\textrm{next}}$で置き換え、2へ戻る。
クラスカル法で求めた$A$の最小全域木を$P$の最頻値を根としてHL分解したものを用いて経路$P_{\textrm{next}}$と$A_{\textrm{next}}$をダイクストラ法の反復で計算する。
$A_{\textrm{next}}$の像のサイズが$A$より小さければ、$A$と経路$P$を$A_{\textrm{next}}$と経路$P_{\textrm{next}}$で置き換え、像のサイズは$A$と同じで経路の重みが減っているならば経路$P$のみ経路$P_{\textrm{next}}$で置き換え、2へ戻る。
$A$と経路$P$を確定させる。

といった処理を行っています。4でHL分解することで$A$の先頭項（座標圧縮のサイズ分）を埋められますが、残りは重複を気にしなくて良いので経路の末尾を逆向きに進んでそのまま$A$に埋めていました。

この「経路の末尾を逆向きに進んで$A$に埋める」という恣意的な部分が何とも微妙です。ここを末尾以外に乱択する？　いや、むしろ残りも未使用の辺を含む最小全域木をHL分解して埋められるだけ埋めるのがいいかも！

提出結果は絶対スコア$68207$で悪化！　今のなし！

$8$回目の提出

冷静に考えて、残りもクラスカル法とHL分解で埋めちゃ乱択じゃないんですよ。こんなんじゃダメです。貪欲法をするからには、もっと貪欲に乱択していかなければ。

というわけで、経路の末尾を逆向きに進んで$A$に埋めるという部分を乱択しようと思います。末尾じゃなくて適用な位置で乱択しようというわけですね。

提出結果は絶対スコアが$66019$です。末尾固定の$65951$より悪化してしまいました。

末尾も一応試してから乱択、というステップにしているのでこれで悪化するということは、末尾でもどこでもON/OFF切り替え回数は全然変わっておらず単に残りのループ時間が削られているとかでしょうね。

$9$回目の提出

というわけで乱択対象を変えます。今はHL分解の根をパスの最頻値にしていますが、ここを乱択にしてみましょう。もちろん先程と同様$1$回目は元の値（最頻値）に固定して悪化しにくいようにして。

提出結果の絶対スコアは$65623$で改善しました。相対スコアは$28,046,292,755$で、順位は112/1041位とキープです。

$10$回目の提出

やはり自環境でTL$10000$[ms]はAtCoder環境のTL$3000$[ms]よりループ回数が少なすぎるので、出力結果をビジュアライザに入れても得らえる情報が少ないです。

そろそろ眠いのでどうせ提出しないので、$25$[m]かかる覚悟で自環境でTL$30000$[ms]にしてサンプル$50$個回してみることにします。

そして改善の代わりに、改善策が尽きた時用の最終提出としてデバッグ出力を全て削除したバージョンを提出しておきます。

あれ？　デバッグ出力を削除したバージョンをコードテストに投げたら、最後まで出力できましたね？　さてはこれ、十分絶対スコアが良い提出に限っては余計なデバッグ出力しなければコードテストで全部出力できたってことですか！？

とりあえず提出結果の絶対スコアは$65537$でした。デバッグ出力を減らした分高速になったのかわずかに改善して、若干きりのいい数字になりましたね。相対スコアは$27,990,100,104$で、順位は114/1043位と少し落ちました。

最終日（9/2月）

駄目元で、評価値にON/OFF切り替え回数そのものを考慮してみたのですがやはり駄目でした。

最小全域木のHL分解を用いた乱択による$A$と経路の更新はその後のUnionFindを用いたソートによる$A$と経路の更新の座標圧縮部分をサポートするために役立つ一方でON/OFF切り替え回数そのものは数倍に膨らませてしまうため、評価値にON/OFF切り替え回数を追加してしまうとすぐに局所最適解に収束してしまいあまり更新できないようです。

$1$回目の提出

ここで気付いたのですが、今の$A$と経路の更新打ち切りは

最小全域木のHL分解を用いた乱択による更新が連続で$30$回失敗したら打ち切り
$2100$[ms]経過したら打ち切り

としていますが、後者の打ち切りの場合最終的な$A$と経路が最小全域木のHL分解を用いた乱択で定めた直後のものになってしまう可能性があります。その場合はON/OFF切り替え回数が膨れ上がってしまうため、最後にもう$1$回UnionFindを用いたソートによる$A$と経路の更新を噛ませることにしました。

提出結果は絶対スコアが$64891$で改善、相対スコアは$27,171,776,602$です。しかし順位は一気に落ちて137/1067位となってしまいました。最終日付近では手元で完結して色々改善できるレベルの強者たちがどんどん提出してくるでしょうから、この後も激しく落ちることが予想されます。

$2$回目の提出

ここからは大幅な変更をしても提出結果でデバッグしていくことが難しいので、コンパイル時定数の微調整をしていこうと思います。

まずは、$A$と経路の更新打ち切り時間を$2100$[ms]から$2400$[ms]に伸ばしてみることにしました。

提出結果は$64606$と僅かに改善。相対スコアは$27,523,620,934$で、順位は129/1069に上がりました。

$3$回目の提出

ここでHL分解の乱択パートにミスを発見。。根を乱択してるつもりが、最初に選んだ最頻点がずっと根に使われ続けるコードになっていました。となると乱択パートで何かが更新されているのがおかしいので実装ミスが他にもあるはずで、よく眺めると$A$のHL分解計算時に$A$の代わりに$A$の最小全域木のHL分解を参照してしまっており、実質二重のHL分解のようになっており意図しない挙動が発生していました。

修正して再提出。残り時間は$4.5$[h]ほどなので、絶対スコアが悪化したら困りますね。。その場合はミスがあることを承知で元に戻すべきでしょうか？

提出結果は絶対スコア$66191$です。案の定悪化！　うわー、どうしよう。

$4$回目の提出

意図しない挙動で点数が上がっていた理由を考えると、$A$が破壊されたことで局所最適解への収束を妨げられたことが考えられます。しかし二重のHL分解は全単射でないので$A$の像が減ってしまい経路が存在しなくなってしまう危険性があるので、このままでは不完全です。

代わりにこの結果を逆用して$A$を現在の経路でなく直前で棄却された経路で埋めたものの最小全域木のHL分解を取って経路の再計算をする、という戦略を取ってみます。

しかし提出結果は絶対スコア$66380$と更に悪化。どうも前の絶対スコアに戻りません。

$5$回目の提出

まだ諦めません。$A$を破壊することで局所最適解への収束が妨げられることから、HL分解後の$A$の先頭項（制限が$A$の像へ全単射になる）に適当な全単射を噛ませて$A$をシャッフルすることでランダム化し続ければいずれ良い乱数を引くかもしれません。

幸い$A$の最小全域木のHL分解はそれ自身が全単射を与えてくれるので、二重のHL分解による破壊と違って経路が必ず存在することが保証されます。乱択ではないですがシャッフルによる疑似乱択！

提出結果の絶対スコアは$65277$で、さっきよりは改善しましたがミスがあった時の$64606$には届きません。このままではミスがあるバージョンを最終提出にすることに……。それは避けたいところです。

$6$回目の提出

HL分解を用いた$A$のシャッフルは$A$の先頭しかシャッフルしないせいで効果が薄かったのだと思います。ミスった提出はもっと全体的に$A$がシャッフルされるので、同様に$A$全体をランダムにシャッフルすることを考えました。

しかし実行エラー！　何か配列に入れた覚えのない負数が入ってます。どこから湧いたゴミでしょうか？　必死にデバッグしたのですが原因が特定できず、残り時間が$1$[h]と$7$[m]になってきました。

仕方ないので二重のHL分解のミスをした提出を少しだけ高速化し提出。残り時間$1$[h]と$3$[m]です。高速化がミスっていてもまだ$1$回提出できます。

結果は絶対スコアが$64702$と、ミスった時の提出の$64606$と近い値に。恐らく乱数のブレが出ただけで高速化のミスではないと信じ、これにて終了します。相対スコアは$27,295,937,561$、提出時点の暫定順位は137/1087位でした。ここからどこまで落ちるかな。

暫定的な入力では通っていますが、最終的な点数計算ではたくさんのテストケースを試すことになるので経路が存在せずREかWAとなるケースもあるかもしれません。その場合は最終的な順位が一気に落ちるでしょう。そういう部分も含めて乱択かな！

以下、C++のソースコードの定義本体部分です。

実際の提出ページはこちらです。

#ifdef DEBUG
  #define INPUT( T , X , Y ) T X , Y; ifs >> X >> Y;
  #define INPUT_ASSERT( X , ... ) int X; ifs >> X
  #define INPUT_A( T , I , N , A ) vector<T> A( I + N ); FOR( i , 0 , N ){ ifs >> A[i+I]; }
  #define OUTPUT ofs
  #define LOCAL( ... ) __VA_ARGS__
#else
  #define INPUT( T , X , Y ) CIN( T , X , Y )
  #define INPUT_ASSERT( X , ... ) CIN_ASSERT( X , __VA_ARGS__ )
  #define INPUT_A( T , I , N , A ) CIN_A( T , I , N , A )
  #define OUTPUT cout
  // #define LOCAL( ... ) __VA_ARGS__
  #define LOCAL( ... ) 
#endif

IN VO Solve()
{

  #ifdef DEBUG
    cout << "ローカルモードで実行します。" << endl;
    int count_sum = 0;
    FOR( sample_num , 0 , 50 ){
      const string sample_num_str = to_string( 10000 + sample_num ).substr( 1 ) + ".txt";
      // const string sample_num_str = to_string( 10000 + sample_num + 50 ).substr( 1 ) + ".txt";
      ofstream ofs{ "C:/Users/user/Desktop/out/" + sample_num_str , ios::trunc };
      ifstream ifs{ "C:/Users/user/Desktop/in/" + sample_num_str , ios::in };
  #else
    CEXPR( int , bound_N , 600 );
    CEXPR( int , bound_T , 600 );
    CEXPR( int , bound_LB , 24 );
  #endif
  

  // VVV 入力
  START_WATCH;
  INPUT_ASSERT( N , bound_N , bound_N );
  INPUT_ASSERT( M , N - 1 , 3 * ( N - 2 ) );
  INPUT_ASSERT( T , bound_T , bound_T );
  INPUT_ASSERT( LA , N , 2 * N );
  INPUT_ASSERT( LB , 4 , bound_LB );
  vector<vector<int>> e( N );
  FOR( j , 0 , M ){
    INPUT( int , u , v );
    e[u].push_back( v );
    e[v].push_back( u );
  }
  INPUT_A( int , 1 , T , target );
  // INPUT_A( T2<int> , 0 , N , xy );
  // AAA 入力


  // VVV 経路前計算
  // O(N^2)
  // appearとnearのみに依存して辺を計算する。
  vector<bool> appear( N , true );
  vector near( N , vector<bool>( N ) );
  const int path_length = LB;
  auto edge = [&]( const int& i ){
    vector<T2<int>> answer{};
    RUN( e[i] , j ){
      if( appear[j] ){
        answer.push_back( { j , near[i][j] ? 1 : path_length } );
      }
    }
    return answer;
  };
  Graph graph{ N , edge };

  // O(T*N(log N+LB))
  auto FillA = [&]( vector<int>& A_next , const int& cc_size_next , const vector<int>& path_next , const int& path_size_next ){
    FOR( i , cc_size_next , LA ){
      A_next[i] = path_next[path_size_next - i - 1 - cc_size_next];
    }
  };

  int cc_size_next , weight_next;
  vector<bool> appear_next{};
  AbstractDijkstra<int,decltype(graph),int,AdditiveMonoid<int>> dijk{ graph , AdditiveMonoid<int>() , LB * ( N - 1 ) * T + 1 };
  // O(TN(log N+LB))
  // nearとappearのみに依存してA_nextとappear_nextとnear_nextとpath_nextとpath_size_nextを計算する。
  auto MutualPathAComputation = [&]( vector<int>& A_ref , vector<vector<bool>>& near_ref , vector<int>& path_ref , int& path_size_ref ){
    path_ref.clear();
    appear_next = vector<bool>( N );
    near_ref = vector( N , vector<bool>( N ) );
    cc_size_next = 0;
    weight_next = 0;
    path_size_ref = 0;
    // O(TN(log N+LB))
    FOR( t , 0 , T ){
      // O(N log N)
      auto [w,p] = dijk.GetPath( target[t] , target[t+1] );
      LOCAL( assert( w != dijk.Infty() ) );
      weight_next += w;
      // O(N*LB)
      p.pop_front();
      RUN( p , i ){
        path_ref.push_back( i );
        if( !appear_next[i] ){
          appear_next[A_ref[cc_size_next] = i] = true;
          // O(LB)
          FOR( i , max( 0 , cc_size_next - LB + 1 ) , cc_size_next ){
            near_ref[A_ref[cc_size_next]][A_ref[i]] = near_ref[A_ref[i]][A_ref[cc_size_next]] = true;
          }
          cc_size_next++;
        }
        path_size_ref++;
      }
    }
    FillA( A_ref , cc_size_next , path_ref , path_size_ref );
  };

  vector<int> A( LA );
  vector<int> path{}; int path_size = 0;
  int cc_size = 0;
  MutualPathAComputation( A , near , path , path_size );
  swap( appear , appear_next );
  int weight = weight_next;
  cc_size = cc_size_next;
  LOCAL( OUTPUT << "#First Dijkstra, time=" << int( CURRENT_TIME ) << ": path_size=" << path_size << ", weight=" << weight << ",cc_size=" << cc_size << endl );
  // AAA 経路前計算


  // VVV 経路最適化
  // O((LA+N)*α(N))
  vector<vector<int>> class_A{};
  // Aをクラス分けする。
  // appearに依存し、nearに依存しない。
  auto ClassifyA = [&](){
    // O(N)
    // 各頂点vに対し、各i in A_inv[v]の連結成分の代表元をrepresentatives[v]に格納する。
    vector representatives( N , set<int>() );
    representatives[0].insert( 0 );
    // O(LA)
    UnionFindForest uff{ LA };
    // O((LA+N)*α(N))
    FOR( i , 1 , LA ){
      auto& r = uff.RootOfNode( i - 1 );
      bool found = false;
      // O(α(N))
      // A[i]自身がi-1の連結成分のAでの像に現れるならば、iもその連結成分に入れる。
      // 各頂点の重複度は基本的に2以下であることを想定していることに注意。
      RUN( representatives[A[i]] , j ){
        if( r == uff.RootOfNode( j ) ){
          uff.Graft( i , r );
          found = true;
          break;
        }
      }
      if( found ){
        continue;
      }
      int adjacent = i;
      // そうでなくA[i]の隣接頂点がi-1の連結成分のAでの像に現れるならば、iもその連結成分に入れる。
      // そうでなくA[i]の隣接頂点が他の連結成分のAでの像に現れるならば、iもその連結成分に入れる。
      // そうでないならば、iのみの連結成分を作る。
      // O(edge( A[i] ).size()*α(N))
      RUN( e[A[i]] , j ){
        if( !appear[j] ){
          continue;
        }
        RUN( representatives[j] , k ){
          adjacent = uff.RootOfNode( k );
          if( adjacent == r ){
            found = true;
            break;
          }
        }
        if( found ){
          break;
        }
      }
      if( adjacent != i ){
        uff.Graft( i , adjacent );
      }
      representatives[A[i]].insert( adjacent );
    }
    // O(LA)
    vector<int> colour( LA , -1 );
    class_A.clear();
    FOR( i , 0 , LA ){
      int& c = colour[uff.RootOfNode( i )];
      if( c == -1 ){
        c = class_A.size();
        class_A.push_back( { i } );
      } else {
        class_A[c].push_back( i );
      }
    }
  };

  // 擬順序であることに注意。
  auto OrderClass = [&]( const vector<int>& c1 , const vector<int>& c2 ){
    return c1.size() >= c2.size();
  };
  
  // O(LA)
  vector<int> A_next( LA );
  // AとA_nextを書き変える。
  // appearとim(A)は変化しないので、appearの更新は不要。
  auto RearrangeA = [&](){
    // O(LA)
    int sort_index = 0;
    RUN( class_A , S ){
      RUN( S , i ){
        A_next[sort_index++] = A[i];
      }
    }
    LOCAL( assert( sort_index == LA ) );
    swap( A , A_next );
  };

  // O((LA+N)*α(N)+class_A.size() log class_A.size())
  // appearに依存し、nearに依存せず、AとA_nextを書き変える。
  // appearとim(A)は変化しないので、appearの更新は不要。
  auto SortA = [&](){
    // O((LA+N)*α(N))
    // appearに依存し、nearに依存しない。
    ClassifyA();
    // O(class_A.size() log class_A.size())
    sort( class_A.begin() , class_A.end() , OrderClass );
    // O(LA)
    // AとA_nextを書き変える。
    RearrangeA();
    // O((LA+N)*α(N))
    // appearに依存し、nearに依存しない。
    ClassifyA();
    // O(LA)
    // AとA_nextを書き変える。
    RearrangeA();
  };

  // O(N^2+LA*LB)
  // nearを書き変える。
  auto UpdateNear = [&](){
    // O(N^2)
    near = vector( N , vector<bool>( N ) );
    // O(LA*LB)
    FOR( i , 0 , LA ){
      const int i_lim = min( LA , i + LB );
      FOR( j , max( 0 , i - LB + 1 ) , i_lim ){
        near[A[i]][A[j]] = true;
      }
    }
  };
  
  int path_size_next;
  bool updated_path_score;
  auto CheckUpdatedPathValue = [&](){
    updated_path_score = T3<int>{cc_size,weight,path_size} > T3<int>{cc_size_next,weight_next,path_size_next};
  };
  
  vector<int> A_opt( LA );
  vector<bool> appear_opt{};
  vector<vector<bool>> near_opt{};
  vector<vector<bool>> near_next{};
  vector<int> path_next{};
  // O(T*N(log N+LB))
  // appearに依存し、nearに依存せず、AとnearとA_nextとappear_nextとnear_nextとpath_nextとpath_size_nextを書き変える。
  // appearとim(A)は変化しないので、appearの更新は不要。
  auto GeneratePathFromSortedA = [&](){
    A_opt = A;
    // O((LA+N)*α(N)+class_A.size() log class_A.size())
    // appearに依存し、nearに依存せず、AとA_nextを書き変える。
    // appearとim(A)は変化しないので、appearの更新は不要。
    SortA();
    swap( near , near_opt );
    // O(N^2+LA*LB)
    // nearを書き変える。
    UpdateNear();
    // O(TN(log N+LB))
    // A_nextとappear_nextとnear_nextとpath_nextとpath_size_nextを書き変える。
    MutualPathAComputation( A_next , near_next , path_next , path_size_next );
    CheckUpdatedPathValue();
  };

  vector<vector<int>> A_inv{};
  // O(LA)
  // appearに依存し、nearに依存せず、A_invを書き変える。
  auto SetAInv = [&](){
    A_inv = vector( N , vector<int>() );
    FOR( i , 0 , LA ){
      LOCAL( assert( appear[A[i]] ) );
      A_inv[A[i]].push_back( i );
    }
  };

  // Aの単射な部分関数の定義域の枚挙をA_invの値の最初の成分で与えたもの。
  vector<int> cc_Dom_A( cc_size );
  // c_Dom_Aの逆写像。
  vector<int> cc_Dom_A_inv( LA , -1 );
  // O(cc_size)
  // A_invに依存する。
  auto SetCCAInv = [&](){
    int cc_index = 0;
    RUN( A_inv , v ){
      if( !v.empty() ){
        cc_Dom_A[cc_Dom_A_inv[v[0]] = cc_index++] = v[0];
      }
    }
    LOCAL( assert( cc_index == cc_size ) );
  };
  
  vector<vector<T3<int>>> de{};
  vector<T2<int>> de_enum{};
  // O(N)
  // appearとnearとA_invに依存する。
  auto EnumDedge = [&](){
    de = vector( cc_size , vector<T3<int>>() );
    de_enum.clear();
    FOR( i , 0 , cc_size ){
      RUN( e[A[cc_Dom_A[i]]] , j ){
        if( appear[j] ){
          LOCAL( assert( !A_inv[j].empty() ) );
          auto& k = cc_Dom_A_inv[A_inv[j][0]];
          LOCAL( assert( k != -1 && k < cc_size ) );
          de[i].push_back( { k , near[A[i]][j] ? 1 : path_length , de_enum.size()  } );
          de_enum.push_back( { i , k } );
        }
      }
    }
  };

  // O(path_size)
  auto MostArrivedPoint = [&](){
    vector<int> path_hind( cc_size );
    RUN( path , v ){
      LOCAL( assert( !A_inv[v].empty() ) );
      path_hind[cc_Dom_A_inv[A_inv[v][0]]]++;
    }
    int answer = -1 , temp = -1;
    FOR( i , 0 , cc_size ){
      if( temp < path_hind[i] ){
        answer = i;
        temp = path_hind[i];
      }
    }
    return answer;
  };

  vector<vector<int>> te{};
  // O(N*α(cc_size+log N))
  // appearに依存し、nearに依存せず、A_invを書き変える。
  auto SetMinimalTotalTree = [&](){
    // O(cc_size)
    // appearに依存し、nearに依存せず、A_invを書き変える。
    SetAInv();
    // O(cc_size)
    // A_invに依存するが、上で書き変え済み。
    SetCCAInv();
    // O(N)
    // appearとnearとA_invに依存する。
    EnumDedge();
    Graph dgraph{ cc_size , Get( de ) };
    // O(N*α(cc_size+log N))
    auto [de_nums,cc_num] = Kruscal( dgraph , de_enum );
    LOCAL( assert( cc_num == 1 ) );
    // O(cc_size)
    te = vector<vector<int>>( cc_size );
    // O(cc_size)
    RUN( de_nums , k ){
      auto& [i,j] = de_enum[k];
      te[i].push_back( j );
      te[j].push_back( i );
    }
  };

  vector<int> shuffle{};
  // O(cc_size log cc_size)
  // appearに依存し、nearに依存せず、AとA_invとA_nextを書き変える。
  // appearとim(A)は変化しないので、appearの更新は不要。
  auto HLDecomposeA = [&]( const int& centre ){
    Graph tree{ cc_size , Get( te ) };
    // O(cc_size log cc_size)
    HeavyLightDecomposition hld{ tree , centre };
    // O(cc_size)
    shuffle.resize( cc_size );
    FOR( i , 0 , cc_size ){
      A_next[i] = A[cc_Dom_A[shuffle[i] = hld.RearragedNodeNumber( i )]];
    }
    swap( A , A_next );
    // O(LA)
    FillA( A , cc_size , path , path_size );
  };

  int centre;
  // appearとnearに依存し、AとA_invとnearとA_nextとappear_nextとnear_nextとpath_nextとpath_size_nextを書き変える。
  auto GeneratePathFromHLDecomposedACentre = [&](){
    A_opt = A;
    // O(N*α(cc_size+log N))
    // appearに依存し、nearに依存せず、A_invを書き変える。
    SetMinimalTotalTree();
    // O(path_size)
    centre = MostArrivedPoint();
    // O(cc_size log cc_size)
    // appearとnearに依存し、AとA_invとA_nextを書き変える。
    // appearとim(A)は変化しないので、appearの更新は不要。
    HLDecomposeA( centre );
    swap( near , near_opt );
    // O(N^2+LA*LB)
    // nearを書き変える。
    UpdateNear();
    // O(TN(log N+LB))
    // A_nextとappear_nextとnear_nextとpath_nextとpath_size_nextを書き変える。
    MutualPathAComputation( A_next , near_next , path_next , path_size_next );
    CheckUpdatedPathValue();
  };

  // O(cc_size log cc_size+N^2+LA*LB+TN(log N+LB))
  auto GeneratePathFromHLDecomposedARandom = [&](){
    swap( A , A_opt );
    FOR( i , 0 , cc_size ){
      A_next[i] = A[cc_Dom_A[shuffle[i]]];
    }
    swap( A , A_next );
    // O(LA)
    FillA( A , cc_size , path , path_size );
    swap( near , near_opt );
    // O(N^2+LA*LB)
    // nearを書き変える。
    UpdateNear();
    // O(TN(log N+LB))
    // A_nextとappear_nextとnear_nextとpath_nextとpath_size_nextを書き変える。
    MutualPathAComputation( A_next , near_next , path_next , path_size_next );
    CheckUpdatedPathValue();
  };
  // AAA 経路最最適化


  // VVV 変数設定
  // O(coeff_size)
  CEXPR( double , nd_scale , 6e6 );
  CEXPR( int , coeff_scale , 1 << 20 );
  CEXPR( int , coeff_noize , 100 );
  CEXPR( decltype( declval<vector<int>>().size() ) , coeff_size_lim , 40 );
  vector<int> coeff( 1 , ( 1 << 24 ) - 1 );
  int coeff_size;
  int nd_rate;
  double nd_point , nd_diff;
  // O(coeff_size)
  auto SetCoeffRate = [&]( const int& rate ){
    nd_rate = rate;
    nd_point = 0.0 , nd_diff = nd_rate / nd_scale;
    coeff.resize( 1 );
    while( coeff.back() != 0 && coeff.size() < coeff_size_lim ){
      nd_point += nd_diff;
      coeff.push_back( coeff[0] * exp( - nd_point * nd_point ) );
    }
    coeff.pop_back();
    coeff_size = coeff.size();
  };
  CEXPR( int , nd_rate_init , nd_scale / 6 );
  SetCoeffRate( nd_rate_init );

  // O(coeff_size)
  auto RandomiseCoeffRate = [&](){
    SetCoeffRate( GetRand( 1 , nd_rate_init * 3 ) );
  };

  // O(coeff_size)
  vector<int> coeff_opt{};
  int coeff_index = 1;
  auto RandomiseCoeff = [&](){
    coeff[coeff_index] = GetRand( 1 , ( coeff_index == 1 ? coeff_scale : coeff[coeff_index-1] ) + coeff_noize );
  };

  vector<int> B{};
  map<int,int> hind_B{};
  auto ResetB = [&](){
    B = vector<int>( LB , -1 );
    hind_B.clear();
  };
  
  int loop_num = 0;
  int phase = 1;
  bool generating_path_from_sorted_A = true;
  bool generating_path_from_HLD_A_centre = false;
  auto SetParameters = [&](){
    loop_num++;
    if( phase == 1 ){
      if( generating_path_from_sorted_A ){
        GeneratePathFromSortedA();
      } else if( generating_path_from_HLD_A_centre ){
        GeneratePathFromHLDecomposedACentre();
      } else {
        GeneratePathFromHLDecomposedARandom();
      }
    } else if( phase == 2 ){
      // O(coeff_size)
      RandomiseCoeffRate();
    } else {
      assert( phase == 3 );
      // O(coeff_size)
      RandomiseCoeff();
    }
    ResetB();
  };
  // AAA 変数設定


  // VVV ON/OFF切り換え貪欲法
  // O(L)
  bool last = false;
  auto UpdateB = [&]( const int& L , const int& i , const int& j ){
    if( last ){
      OUTPUT << "s " << L << " " << i << " " << j << "\n";
    }
    FOR( l , 0 , L ){
      if( B[j+l] != -1 ){
        auto itr = hind_B.lower_bound( B[j+l] );
        if( --itr->second == 0 ){
          hind_B.erase( itr );
        }
      }
      hind_B[B[j+l] = A[i+l]]++;
    }
  };

  // O(LB)
  auto FillB = [&]( const int& v ){
    auto begin = A_inv[v].begin() , itr = --A_inv[v].end();
    int i = *itr;
    while( i + LB > LA ){
      if( itr != begin ){
        i = *--itr;
      } else {
        i = LA - LB;
      }
    }
    UpdateB( LB , i , 0 );
  };

  // パス上coeff_size以内に登場予定の頂点番号のpathによる逆像を管理。
  // 区間の右端取得にはパス上L_B以内だけで良いが、評価値の計算にcoeff_size以内まで用いる。
  vector<set<int>> next_occur{};
  // パス上coeff_size以内での評価値の値の総和を頂点番号ごとに管理。
  vector<int> next_value{};
  auto count_hit_B = [&]( const int& j ){ return next_value[B[j]]; };
  // O(LB+mult_B.size()^2 log mult_B.size()+hit_B_nontriv*coef_size log coef_size)
  auto IntervalSumMinB = [&](){
    // path上で現在位置からcoeff_sizeまでにBの成分が出現する頻度を管理。
    // 区間の右端取得のためのnumをここで挿入してしまうとvalueの管理が正しくできないので
    // 代わりにUpdateGreedyValueの計算時に行う。
    map<int,int> mult_B{};
    // path上で現在位置からcoeff_sizeまでにB[j]が出現するj全体を管理。
    vector<int> B_occur = {-1};
    int total_value = 0;
    // O(LB+mult_B.size() log mult_B.size())
    // Bの成分の重複は基本的に2以下であることに注意。
    FOR( j , 0 , LB ){
      if( count_hit_B( j ) > 0 ){
	if( mult_B[B[j]]++ == 0 ){
	  total_value += count_hit_B( j );
	}
	B_occur.push_back( j );
      }
    }
    const int B_occur_size = B_occur.size();
    B_occur.push_back( LB );
    // O(LB)
    // {残る集合,残る評価値の最大値,左端}を管理。
    vector<tuple<LineSubset<int>,int,int>> answer( LB + 1 , { LineSubset<int>{} , -1 , -1 } );
    // O(mult_B.size()^2 log mult_B.size())
    FOR( s , 0 , B_occur_size ){
      int t = s;
      int L = B_occur[++t] - B_occur[s] - 1;
      // 評価値0の連続部分列を除くので全体の評価値が残る。
      int value = get<1>( answer[L] ) = total_value;
      get<2>( answer[L] ) = B_occur[s] + 1;
      // 除く連続部分列における頻度表を尺取り法で管理。
      map<int,int> mult_B_sub{};
      // O(mult_B.size() log mult_B.size())
      while( t < B_occur_size ){
        if( ++mult_B_sub[B[B_occur[t]]] == mult_B[B[B_occur[t]]] ){
          value -= count_hit_B( B_occur[t] );
        }
        L = B_occur[++t] - B_occur[s] - 1;
        auto& [S,value_max_L,j_L] = answer[L];
        if( value_max_L < value ){
          value_max_L = value;
	  j_L = B_occur[s] + 1;
        }
      }
    }
    int value = -1;
    // O(LB+hit_B_nontriv*coef_size log coef_size)
    // hit_B_nontrivはanswerの最終的な非自明成分の個数。
    // 長さと評価値の積順序で極大でない候補を枝刈りする。
    FOREQINV( L , LB , 1 ){
      auto& [S_L,value_max_L,j_L] = answer[L];
      if( value_max_L != -1 ){
        if( value < value_max_L ){
          value = value_max_L;
          const int j_start[2] = {0,j_L+L} , j_lim[2] = {j_L,LB};
          FOR( c , 0 , 2 ){
            FOR( j , j_start[c] , j_lim[c] ){
              if( count_hit_B( j ) > 0 ){
                RUN( next_occur[B[j]] , num_next ){
                  S_L.insert( num_next );
                }
              }
            }
          }
        } else {
	  value_max_L = -1;
	  j_L = -1;
	}
      }
    }
    return answer;
  };
  
  // 合計O((coeff_size+Q)log coeff_size)
  auto count_hit_A = [&]( const int& i ){ return next_value[A[i]]; };
  auto InsertHit = [&]( const int& i , LineSubset<int>& S , int& value ){
    auto& occur_i = next_occur[A[i]];
    if( !occur_i.empty() && !S.find( *occur_i.begin()) ){
      RUN( occur_i , num_next ){
        S.insert( num_next );
      }
      value += count_hit_A( i );
    }
  };

  // 合計O((coeff_size+Q)log coeff_size)
  auto EraseHit = [&]( const int& i , const int& num , LineSubset<int>& S , int& value ){
    auto& occur_i = next_occur[A[i]];
    if( !occur_i.empty() && S.find( *occur_i.begin()) ){
      RUN( occur_i , num_next ){
        S.erase( num_next );
      }
      value -= count_hit_A( i );
    }
  };

  // O(log coeff_size)
  auto UpdateGreedyValue = [&]( const int& num , T4<int>& temp , const LineSubset<int>& S , const int& value , const int& L , const int& i_left ){
    temp = max( temp , T4<int>{ S.find( num ) ? S.ConnectedComponentOf( num ).second : num , value , L , i_left } );
  };

  // O((coeff_size+LB)log coeff_size)
  auto IntervalSumMaxA = [&]( const int& num , const int& i , const vector<tuple<LineSubset<int>,int,int>>& hit_B ){
    // {始端numから到達できる最遠点,評価値,長さ,左端}
    T4<int> answer{};
    FOREQ( L , 1 , LB ){
      auto& hit_B_L = hit_B[L];
      int value = get<1>( hit_B_L );
      if( value == -1 ){
        continue;
      }
      // O(coeff_size)
      LineSubset<int> S = get<0>( hit_B_L );
      const int i_left_min = max( 0 , i + 1 - L );
      // O((coeff_size+L)log coeff_size)
      FOR( l , 0 , L ){
        InsertHit( i_left_min + l , S , value );
      }
      // O(log coeff_size)
      UpdateGreedyValue( num , answer , S , value , L , i_left_min );
      const int i_left_lim = min( LA - L , i + 1 );
      // 平均O((coeff_size+L)log coeff_size)
      // A内の重複が多くは2以下であることに注意。
      FOR( i_left , i_left_min + 1 , i_left_lim ){
        if( A[i_left-1] != A[i_left+L-1] ){
          EraseHit( i_left - 1 , num , S , value );
          InsertHit( i_left + L - 1 , S , value );
          UpdateGreedyValue( num , answer , S , value , L , i_left );
        }
      }
    }
    return answer;
  };

  // O((coeff_size+LB)log coeff_size)
  auto OptimiseB = [&]( const int& num , const int& v ){
    // O(LB+coeff_size log coeff_size)
    auto hit_B = IntervalSumMinB();
    T4<int> hit_opt{};
    LOCAL( assert( !A_inv[v].empty() ) );
    // A_inv[v]のsizeは基本的に1か2であることに注意。
    RUN( A_inv[v] , i ){
      // O((coeff_size+LB)log coeff_size)
      hit_opt = max( hit_opt , IntervalSumMaxA( num , i , hit_B ) );
    }
    const int& L = get<2>( hit_opt );
    const int& i = get<3>( hit_opt );
    const int& j = get<2>( hit_B[L] );
    LOCAL( assert( L != 0 && j != -1 ) );
    // O(LB)
    UpdateB( L , i , j );
  };
  // AAA ON/OFF切り換え貪欲法


  // VVV 操作シミュレーション
  // O(coeff_size)
  auto UpdateNextValue = [&]( const int& num , const int& v ){
    next_occur[v].erase( num );
    next_value[v] -= coeff[0];
    const int i_ulim = min( coeff_size , path_size - num );
    FOR( i , 1 , i_ulim ){
      next_value[path[num + i]] += coeff[i - 1] - coeff[i];
    }
    if( num + coeff_size < path_size ){
      next_occur[path[num + coeff_size]].insert( num + coeff_size );
      next_value[path[num + coeff_size]] += coeff[coeff_size - 1];
    }
  };

  // O((coeff_size+LB)log coeff_size)
  int count;
  auto SetOperation = [&]( const int& num ){
    const int& v = path[num];
    if( hind_B.count( v ) == 0 ){
      count++;
      if( B[0] == -1 ){
        // O(LB)
        FillB( v );
      } else {
        // O((coeff_size+LB)log coeff_size)
        OptimiseB( num , v );
      }
    }
    if( last ){
      OUTPUT << "m " << v << "\n";
    }
    // O(coeff_size)
    UpdateNextValue( num , v );
  };

  // O(path_size(coeff_size+LB)log coeff_size)
  auto SimulateTavel = [&](){
    count = 0;
    // O(N)
    next_occur = vector( N , set<int>() );
    next_value = vector<int>( N );
    // O(coeff_size)
    FOR( num , 0 , coeff_size ){
      next_occur[path[num]].insert( num );
      next_value[path[num]] += coeff[num];
    }
    // O(path_size(coeff_size+LB)log coeff_size)
    FOR( num , 0 , path_size ){
      // O((coeff_size+LB)log coeff_size)
      SetOperation( num );
    }
  };
  // AAA 操作シミュレーション


  // VVV 最適変数管理
  int HLD_A_random_count = 0;
  auto ChoosePathAndNextA = [&](){
    if( generating_path_from_sorted_A ){
      LOCAL( OUTPUT << "#Chose path from sorted A at trial " );
      HLD_A_random_count = 0;
    } else if( generating_path_from_HLD_A_centre ){
      LOCAL( OUTPUT << "#Chose path from HLD A centre at trial " );
      generating_path_from_sorted_A = true;
      generating_path_from_HLD_A_centre = false;
      HLD_A_random_count = -1;
    } else {
      LOCAL( OUTPUT << "#Chose path from HLD A random at trial " );
      generating_path_from_sorted_A = true;
      HLD_A_random_count = -1;
    }
    LOCAL( OUTPUT << loop_num << ", phase " << phase << ", time=" << int( CURRENT_TIME ) << ": weight(chmax)=" << weight_next << ", path_size=" << path_size_next << ", cc_size=" << cc_size_next << endl );
    swap( A , A_next );
    swap( near , near_next );
    // im(A)が変化しうるので、appearも更新する。
    swap( appear , appear_next );
    swap( path , path_next );
    // weight_nextは元のAと新しいpathに対するものなのでmaxに置き換える。
    weight = max( weight , weight_next );
    swap( path_size , path_size_next );
    swap( cc_size , cc_size_next );
  };
  
  auto ChoosePathAndCurrentA = [&](){
    if( generating_path_from_sorted_A ){
      LOCAL( OUTPUT << "#Chose path from sorted A at trial " );
      generating_path_from_sorted_A = false;
      generating_path_from_HLD_A_centre = true;
      HLD_A_random_count = 0;
    } else if( generating_path_from_HLD_A_centre ){
      LOCAL( OUTPUT << "#Chose path from HLD A centre at trial " );
      generating_path_from_sorted_A = true;
      generating_path_from_HLD_A_centre = false;
      HLD_A_random_count = -1;
    } else {
      LOCAL( OUTPUT << "#Chose path from HLD A random at trial " );
      generating_path_from_sorted_A = true;
      HLD_A_random_count = -1;
    }
    LOCAL( OUTPUT << loop_num << ", phase " << phase << ", time=" << int( CURRENT_TIME ) << ": weight=" << weight_next << ", path_size=" << path_size_next << ", cc_size(unchanged)=" << cc_size_next << endl );
    // im(A)が変化しないので、appearは更新しない。
    swap( path , path_next );
    swap( weight , weight_next );
    swap( path_size , path_size_next );
    LOCAL( assert( cc_size == cc_size_next ) );
  };

  auto DeclinePathGeneratedFromSortedA = [&](){
    LOCAL( OUTPUT << "#Declined path generated from sorted A at trial " << loop_num << ", phase " << phase << ", time=" << int( CURRENT_TIME ) << ": weight(declined)=" << weight_next << ", path_size(declined)=" << path_size_next << ", cc_size(declined)=" << cc_size_next << endl );
    swap( A , A_opt );
    swap( near , near_opt );
    generating_path_from_sorted_A = false;
    generating_path_from_HLD_A_centre = true;
  };

  auto DeclinePathGeneratedFromHLDACentre = [&](){
    LOCAL( OUTPUT << "#Declined path generated from HLD A centre at trial " << loop_num << ", phase " << phase << ", time=" << int( CURRENT_TIME ) << ": weight(declined)=" << weight_next << ", path_size=" << path_size_next << ", cc_size=" << cc_size_next << endl );
    swap( A , A_opt );
    swap( near , near_opt );
    generating_path_from_HLD_A_centre = false;
  };

  auto DeclinePathGeneratedFromHLDARandom = [&](){
    LOCAL( OUTPUT << "#Declined path generated from HLD A random at trial " << loop_num << ", phase " << phase << ", time=" << int( CURRENT_TIME ) << ": weight(declined)=" << weight_next << ", path_size=" << path_size_next << ", cc_size=" << cc_size_next << endl );
    swap( A , A_opt );
    swap( near , near_opt );
    HLD_A_random_count++;
  };
  
  // O(LA)
  auto SetPathOpt = [&](){
    if( updated_path_score ){
      // (1) ソートしたAによるパスとA_nextの再計算。
      //     -> 成功時Aとパスを更新して再度(1)へ、失敗時(2)へ。
      // (2) HL分解したAによるパスの重み再計算。
      //     -> 成功時Aを更新してパスからA_nextを再計算し(1)へ、失敗時終了。
      if( cc_size > cc_size_next ){
        ChoosePathAndNextA();
      } else {
        ChoosePathAndCurrentA();
      }
    } else {
      if( generating_path_from_sorted_A ){
        DeclinePathGeneratedFromSortedA();
      } else if( generating_path_from_HLD_A_centre ){
        DeclinePathGeneratedFromHLDACentre();
      } else {
        DeclinePathGeneratedFromHLDARandom();
      }
    }
  };
  
  CEXPR( int , count_bound , 1e5 );
  int count_min = count_bound;
  int nd_rate_opt = nd_rate_init;
  auto UpdateOpt = [&](){
    count_min = count;
    if( phase == 2 ){
      nd_rate_opt = nd_rate;
      LOCAL( OUTPUT << "#Update at trial " << loop_num << ", phase " << phase << ": count=" << count << ", nd_rate=" << nd_rate << ", coeff_size=" << coeff_size << endl );
    } else {
      LOCAL( assert( phase == 3 ) );
      coeff_opt[coeff_index] = coeff[coeff_index];
      LOCAL( OUTPUT << "#Update at trial " << loop_num << ", phase " << phase << ", coeff_index " << coeff_index << ": count=" << count << ", nd_rate=" << nd_rate << ", coeff_size=" << coeff_size << ", coeff=["; FOREQ( i , 0 , coeff_index ){ OUTPUT << coeff[i] << ",]"[i==coeff_index]; } OUTPUT << endl );
    }
  };

  int coeff_index_last = 1;
  // 合計O(coeff_size)
  auto SetCoeffOpt = [&](){
    FOR( i , coeff_index_last , coeff_index ){
      coeff[i] = coeff_opt[i];
    }
  };
  // AAA 最適変数管理


  // VVV フェーズ更新
  // CEXPR( int , TL , 3000 );
  // DEXPR( int , TL , 3000 , 10000 );
  DEXPR( int , TL , 3000 , 30000 );
  CEXPR( int , phase2_3_rate_n , 1 );
  CEXPR( int , phase2_3_rate_d , 4 );
  int phase1_finished;
  int phase3_start;
  int loop_num_1;
  // O(LA)
  auto FinishPhase1 = [&](){
    // O(LA)
    SetAInv();
    appear.clear();
    A_next.clear();
    A_opt.clear();
    appear_next.clear();
    appear_opt.clear();
    near.clear();
    near_next.clear();
    near_opt.clear();
    path_next.clear();
    class_A.clear();
    cc_Dom_A.clear();
    cc_Dom_A_inv.clear();
    de.clear();
    de_enum.clear();
    phase = 2;
    phase1_finished = int( CURRENT_TIME );
    phase3_start = phase1_finished + ( TL - phase1_finished ) * phase2_3_rate_n / phase2_3_rate_d;
    loop_num_1 = loop_num;
    LOCAL( OUTPUT << "#trial " << loop_num << ", phase 1 -> 2, time=" << int( CURRENT_TIME ) << endl );
  };

  auto LoopNum2 = [&](){
    return loop_num - loop_num_1;
  };
  
  CEXPR( int , loop_num_block , 30 );
  CEXPR( int , phase2_start , TL * 80 / 100 );
  int coeff_index_max;
  // O(coeff_size)
  auto SetCoeffRateOpt = [&](){
    // O(coeff_size)
    SetCoeffRate( nd_rate_opt );
    phase = 3;
    const int loop_num_3 = LoopNum2() * ( TL - phase3_start ) / max( 1 , ( phase3_start - phase1_finished ) );
    coeff_index_max = min( coeff_size - 1 , loop_num_3 / loop_num_block );
    coeff_opt = coeff;
  };

  // O(coeff_size)
  auto FinishPhase2 = [&](){
    // O(coeff_size)
    SetCoeffRateOpt();
    LOCAL( OUTPUT << "#trial " << loop_num << ", phase 2 -> 3, time=" << int( CURRENT_TIME ) << ", coeff_index=" << coeff_index << ", coeff_index_max=" << coeff_index_max << ", coeff_size=" << coeff_size << ": nd_rate=" << nd_rate << ", coeff=[" << coeff[0] << "," << coeff[1] << "]" << endl );
  };

  // 合計O(coeff_size)
  auto UpdateCoeffIndex = [&](){
    coeff_index_last = coeff_index;
    coeff_index = max( 1 , min( int( ( CURRENT_TIME - phase3_start ) * coeff_index_max / ( TL - 100 - phase3_start ) + 1 ) , coeff_size - 1 ) );
    if( coeff_index_last != coeff_index ){
      // 合計O(coeff_size)
      SetCoeffOpt();
      LOCAL( OUTPUT << "#trial " << loop_num << ", phase " << phase << ", coeff_index " << coeff_index_last << " -> " << coeff_index << ", time=" << int( CURRENT_TIME ) << ": nd_rate=" << nd_rate << ", coeff=["; FOREQ( i , 0 , coeff_index ){ OUTPUT << coeff[i] << ",]"[i==coeff_index]; } OUTPUT << endl );
    }
  };

  CEXPR( int , HLD_A_random_count_lim , 30 );
  auto CheckCurrentTime = [&](){
    if( phase == 1 ){
      if( ( CURRENT_TIME > phase2_start && HLD_A_random_count != -1 ) || HLD_A_random_count >= HLD_A_random_count_lim ){
        // O(LA)
        FinishPhase1();
      }
    } else if( phase == 2 ){
      if( CURRENT_TIME > phase3_start || LoopNum2() >= loop_num_block ){
        // O(coeff_size)
        FinishPhase2();
      }
    } else if( phase == 3 ){
      // 合計O(coeff_size)
      UpdateCoeffIndex();
    }
  };
  // AAA フェーズ更新


  // VVV ループ本体
  while( CHECK_WATCH( TL ) ){
    SetParameters();
    if( phase == 1 ){
      // O(LA)
      SetPathOpt();
    } else {
      // O(path_size(coeff_size+LB)log coeff_size)
      SimulateTavel();
      if( count_min > count ){
        UpdateOpt();
      }
    }
    // O(phase==1?N^2+LA*LB:coeff_size)
    CheckCurrentTime();
  }
  // AAA ループ本体


  // VVV 操作実行
  coeff_index = coeff_size;
  if( phase == 1 ){
    SetAInv();
  } else if( phase == 2 ){
    SetCoeffRateOpt();
  } else if( phase == 3 ){
    SetCoeffOpt();
  }
  ResetB();
  LOCAL( OUTPUT << "#Last trial " << loop_num << ": count=" << count_min << ", nd_rate=" << nd_rate << ", coeff_size=" << coeff_size << ", coeff=[" << coeff << "]" << endl );
  last = true;
  // O(N)
  FOR( i , 0 , LA ){
    OUTPUT << A[i] << " \n"[i==LA-1];
  }
  // O(path_size(coeff_size+LB)log coeff_size)
  SimulateTavel();
  LOCAL( assert( count_min == count_bound || count_min == count ) );
  LOCAL( assert( count + path_size <= count_bound ) );
  // AAA 操作実行


  #ifdef DEBUG
      count_sum += count;
      cout << sample_num << ": " << count << endl;
    }
    cout << "total: " << count_sum << endl;
  #endif
}

まとめ

最初は$A$を先頭から経路で埋めつつ、同時に経路は$A$に既に埋まっている情報からダイクストラ法で決めていく。ただし$A$に経路をそのまま埋めようとすると経路の最後の方でだけ出てくる頂点が漏れてしまうので重複しすぎないように調整する。
次に$A$と経路の更新を以下のループで繰り返す。
1. まずUnionFindを用いて$A$をクラス分けし、それを用いて$A$をソートする。これにより、$A$にバラバラに出てくる頂点をなるべくまとめ上げる。
2. 次にソート済みの$A$から経路を再計算する。経路の評価値が良ければ、$A$と経路を更新する。悪ければ、$A$をソート前のものに戻して経路も更新しない。
3. 評価値の推移を見て適宜$A$に現れる頂点のなす部分グラフの最小全域木のHL分解を用いて$A$を変更してみて、経路を再計算する。経路の評価値が良ければ、$A$と経路を更新する。悪ければ、$A$をHL分解前のものに戻して経路も更新しない。
4. 評価値の推移を見て適宜HL分解後の$A$にHL分解から定まる変換を再度施して$A$をシャッフルしてみて、経路を再計算する。経路の評価値が良ければ、$A$と経路を更新する。悪ければ、$A$をHL分解前のものに戻して経路も更新しない。
5. 経路の評価値は像の濃度（座標圧縮のサイズ）と経路の重みと経路の辺の重複を込めた本数に辞書式順序を入れて定め、特に像の濃度が広義単調減少になるように頂点を削除していく。
$A$と経路を確定させたら、実際の操作を貪欲法で計算する。
1. 貪欲法に用いる評価関数は、経路上の現在位置から離れた点の寄与を正規分布上の点群を用いて計算する。
2. 長さと評価関数の値の積順序に関して極大な連続部分列の組み合わせ（一意でないので全パターン）を$A$と$B$から選ぶ。
3. 選んだそれぞれに対して$1$回のON/OFF切り替えで現在位置からどこまで遠くに行けるか（最遠点）を考え、最遠点の遠さと連続部分列の長さに関する辞書式順序で最大なものを選択する。
4. 正規分布のスケールと点群の選び方を変えるごとに評価関数を変わり、選択される連続部分列の組み合わせも変わり、最終的なON/OFF切り替え回数も変わる。そこでそれらを乱択する多段階推定により、ON/OFF切り替え回数の最小化を目指す。
最後に、最もON/OFF切り替え回数が小さくなった正規分布のスケールと点群の選び方に対して操作を実行する。

順位発表

AC×1999、RE×1で、相対スコアは$1,150,034,522,172$、最終順位は146/ 1094位でした！

最終順位表

やっぱりRE出ちゃいましたね。二重のHL分解による$A$の破壊は経路の存在を保証しなくするギャンブルで失敗確率が評価できていなかったので、結果的にRE×1で済んでラッキーです。乱択以外にもギャンブルもヒューリスティックのテクニックとして身につけられました。

感想戦

初参加させていただいたAHCは予想通りとても楽しかったです。いつかAtCoderの長期コンに出てみたいなあと思っていたので、願いが叶ってよかったです。ただ繁忙期と重なっていた事情もあり、とても疲れました。しばらくはお腹いっぱいかな……！

その他の感想：

スコアコンの知識がないので手も足も出ないかもしれないという不安が当初はありましたが、乱択のお陰で色々と手掛かりをつかめたのが大きかったです。全体的に普通の数学の知識が使いやすい問題設定だったのも助かりました。
最初ビジュアライザが重すぎてフリーズ多発してしまったのが辛かったです。改善されていない出力だとサイズが大きすぎるのが原因のようで、そのことに気付かずビジュアライザの使用を途中で断念していました。上位陣の出力なら短くてスイスイなのでしょうけど。
ビジュアライザの録画機能が壊れていることを早期にclarできたことが一番の貢献かもしれません。ただ直ったというアナウンスがあった後も、録画は数十秒ほどでできたものの再生すると飛び飛びの紙芝居のようになってしまい結局役に立ちませんでした……。ファイル容量も大きすぎるようでtwitterに貼れず、終了後のワイワイがしにくいですね。
最初コードテストが出力を打ち切ってしまうことに気付かず、何度ビジュアライザに投げても不正な出力になってしまっていて絶望していました。これも上位陣の出力なら打ち切られずに済むのでしょうけど。
手元でサンプルを回せるようにしたら一気に見通しが良くなったので、早めにそうすると良いと思いました。同じコードでも自環境ではサンプルを回して提出時は入力を受け取る、という挙動をするように最初から思いつけたのが良かったです。一方でassertやデバッグ出力は後でそのように書き直すことになったので、なるべく色々な可能性を考えたコーディングをすべきでした。
過去問をupsolveした時にも思ったことですが、gdbがラムダ式を適切にデバッグできない問題が困りました。コードが長くなるスコアコンではデバッグのしにくさが致命的なので、ラムダ式をやめて関数にすべき？　ただ関数にすると散らかってしまい見にくいのが難点です。
今回は$A$と経路の計算ステップと貪欲法による連続部分列の計算ステップと正規分布の乱択ステップを分けて実装していたのですが、試しに$A$と経路の計算ステップで貪欲法による連続部分列の計算ステップを流用してみようと思うと宣言エラーが大量に出てしまうという問題に直面しました。関数を呼ぶ順番を入れ替える可能性がある長期コンでは変数を全部globalに置いて関数の前方宣言もすべき？
最後にシャッフルの実行エラーが取れずに結局ミスのある不完全な提出を最終提出にすることになったのが悔しかったです。デバッグ速度上げたいなぁ。